Definición
Dada una función \(f:D\to \mathbb{R}\) un periodo para \(f\) es un escalar \(T\ne 0\) para el cual \[ f(x+T)=f(x) \] para todo \(x\in D\) (donde se entiende que \(x+T\in D\) también). También se sigue que si \(T\) es un periodo de \(f\) entonces todo número de la forma \(kT\), \(k=1,2,\) también es un periodo, asi que el periodo no es único.
Una función se llama periódica si tiene tiene un periodo. Si \(f\) es una función periódica y existe un periodo \(T_0\) para el cual \(T_0\leq T\) para cualquier otro periodo positivo \(T\), a \(T_0\) le llamamos periodo fundamental o básico.
Por ejemplos las funciones \(\sen,\cos\) y \(\tan\) tienen periodo fundamental \(2\pi\).
Notas:
Si \(f\) tiene periodo \(T\) y tenemos la gráfica de \(f\) en el intervalo \([a.a+T]\) entonces la gráfica se repite en todo los intervalos siguientes: \([a+T,a+2T],[a+2T,a+3T],\dots\).
Si la función \(f\) es integrable en un intervalo de la forma \([a,a+T]\) entonces es integrable en todo intervalo de la forma \([a+kT,a+(k+1)T]\) y \[ \int_a^{a+T}f(x)dx=\int_{a+kT}^{a+(k+1)T}f(x)dx. \]
Ejercicio
Si \(f:\mathbb{R}\to \mathbb{R}\) tiene periodo \(T\) prueba que \[ f(x)=f(x-kT) \] para todo \(k\in \mathbb{N}\).
Ejercicio
Sea \(T\in \mathbb{R}\), \(T\ne 0\), fijo y denotamos por \(V\) a todas la funciones de \(\mathbb{R}\) en \(\mathbb{R}\) con periodo \(T\). Prueba:
- \(V\) un espacio vectorial y contiene a todas las funciones constantes.
- \(V\) es una subalgebra de funciones.
- \(V\) es una retícula.
Definición
Una función de la forma \[ f(x)=A\sen(\omega x + \theta ) \] donde \(A,\omega, \theta\) son constantes, con \(\omega \ne 0\), se llama armónica básica de amplitud \(|A|\), frecuencia \(\omega\) y fase inicial \(\theta\).
Nota: siempre podemos pedir \(\omega > 0\) pues si no es así podemos reescribir \(A\sen(\omega x + \theta)=-A\sen(-\omega x - \theta)\).
El periodo fundamental de ésta función es \(T=\frac{2\pi}{\omega}\).
Ejercicio
- Prueba que la función \(\cos(x)\) puede escribirse como una función armónica básica.
- Prueba que toda función armónica básica \(A\sen(\omega x +\theta )\) puede escribirse de la forma \[ a\cos(\omega x)+ b \sen(\omega x) \] para ciertas constantes \(a,b\).
- Inversamente toda función de la forma \(a\cos(\omega x)+ b\sen(\omega x)\) puede escribirse como una función armónica básica con periodo fundamental \(T=\frac{2\pi}{\omega}\).
Sugerencia: usa las fórmulas para el seno y coseno de una suma.
Definición
Una función de la forma \[ a_0+\sum_{k=1}^n \left( a_k\cos\left(\frac{k\pi}{l}x\right)+ b_k\sin\left(\frac{k\pi}{l}x\right) \right) \] donde \(a_n^2+b_n^2\neq 0\) (es decir, \(a_n\ne 0\) ó \(b_n\ne 0\)) se llama un polinomio trigonométrico de orden \(n\) y periodo \(2l\).
Si \[ s(x)=a_0+ \sum_{k=1}^n \left(a_k\cos\left(\frac{k\pi}{l}x\right)+ b_k\sin\left(\frac{k\pi}{l}x\right) \right) \] es un polinomio trigonométrico de periodo \(2l\) entonces la función \[ \sigma(t)=s\left(\frac{lt}{\pi}\right)=a_0+\sum_{k=1}^n \left( a_k\cos(kt)+b_k\sen(kt)\right) \] es un polinomio trigonométrico de periodo \(2\pi\). Inversamente si \(\sigma(t)\) es un polinomio trigonométrico de periodo \(2\pi\) entonces \(s(x)=\sigma(\pi x/l)\) es un polinomio trigonométrico de periodo \(2l\). Así pues es equivalente estudiar polinomios trigonométricos de cualquier periodo así que no enfocaremos en aquellos con periodo \(2\pi\).
Ejemplos de polinomios trigonométricos, de grado menor o igual a 3.
Ejercicio
Sea \(\mathcal{T}\) el conjunto de polinomios trigonométricos de periodo \(2\pi\). Es decir \(s\in \mathcal{T}\) si y sólo si existe \(n\in \mathbb{N}, a_0,a_1,\dots, a_n, b_1,\dots, b_n \in \mathbb{R}\) tal que \[ s(x)=a_0+\sum_{k=1}^n \left( a_k\cos(kx)+b_k\sen(kx)\right) \]
Prueba que \(\mathcal{T}\) es una subálgebra de funciones que no se anula en \([-\pi,\pi]\).
Ejercicio
Sea \(\mathcal{T}\) el conjunto de polinomios trigonométricos de periodo \(2\pi\).
Por \(C^{2\pi}(\mathbb{R})\) denotamos al conjunto de funciones continuas de \(\mathbb{R}\) en \(\mathbb{R}\) de periodo \(2\pi\).
Entonces \(\mathcal{T}\) es uniformemente denso en \(C^{2\pi}(\mathbb{R})\). Es decir, para toda función continua y de periodo \(2\pi\), \(f:\mathbb{R}\to \mathbb{R}\), existe \(s \in \mathcal{T}\) tal que \[ \|f-s\|_{[-\pi,\pi]}< \varepsilon. \]
Notas
- Por la periodicidad de las funciones el intervalo \([-\pi,\pi]\) en el resultado anterior se puede cambiar por cualquier otro intervalo de longitud \(2\pi\).
- Este teorema dice que podemos aproximar funciones de periodo \(2\pi\) con polinomios trigonométricos. Las series de Fourier van más allá pues dan condiciones y un método para poder hacer esta aproximación. La llave para poder calcular las aproximaciones son las relaciones de ortogonalidad.
Definición
El sistema trigonométrico básico es conjunto de funciones \[ \{1\}\cup \{\cos(kt) : k\in \mathbb{N}\}\cup \{\sen(kt): k\in \mathbb{N}\} \] Es importante notar que todas estas funciones tienen \(2\pi\) como periodo y es una base para los polinomios trigonométricos de periodo \(2\pi\).
Proposición
Relaciones de ortogonalidad
Para \(n\) un entero distinto de cero:
- \[ \int_{-\pi}^{\pi} \cos(nt)dt=0 \]
- \[\int_{-\pi}^{\pi} \sen(nt)dt=0 \]
Para \(n\ne m\) enteros:
- \[ \int_{-\pi}^{\pi} \cos(nt)\cos(mt)dt=0 \]
- \[ \int_{-\pi}^{\pi} \sen(nt)\sen(mt)dt=0 \]
Para \(n,m\) enteros distintos de cero cualesquiera:
- \[\int_{-\pi}^{\pi} \cos(nt)\sen(mt)dt=0 \]
Para \(n\) un entero distinto de cero:
- \[ \int_{-\pi}^{\pi}\cos^2(nt)dt=\pi \]
- \[ \int_{-\pi}^{\pi}\sen^2(nt)dt=\pi \]
Definición
Dos funciones \(f,g:[a,b]\to \mathbb{R}\) integrables se llaman ortogonales si \[ \int_{a}^b f(t)g(t)dt=0 \]
Con esta nomenclatura la Proposición 7.8 dice que las funciones del sistema trigonométrico básico son ortogonales dos a dos.
Definición
Dada \(f:[a,b]\to \mathbb{R}\) una función integrable se definen los coeficientes de Fourier, con respecto al sistema trigonométrico básico, como \[ \begin{eqnarray*} a_0&=&\frac{1}{\pi} \int_{-\pi}^{\pi} f(t)dt \\ a_k&=&\frac{1}{\pi}\int_{-\pi}^{\pi} f(t)\cos(kt)dt \\ b_k&=&\frac{1}{\pi}\int_{-\pi}^{\pi} f(t)\sen(kt)dt \\ \end{eqnarray*} \] Nota: la misma fórmula para \(a_k\) funciona para \(a_0\) (pues \(\cos(0)=1\)) pero se puso aparte para enfatizar que \(a_0\) da el término constante del polinomio trigonométrico que más adelante se convertirá en la serie de Fourier.
¿Porqué se definen así los coeficientes de Fourier? Una respuesta la da el siguiente teorema.
Teorema
Supongamos que la función \(f(x)\) se puede aproximar con un límite de polinomio trigonométricos de la forma \[ f(x)=\frac{\alpha_0}{2}+\sum_{k=1}^\infty \left( \alpha_k\cos(kx)+\beta_k\sen(kx) \right) \] donde la convergencia es uniforme en \([-\pi,\pi]\). Es decir la sucesión \((s_n)_{n=1}^\infty\) converge uniformemente a \(f\) en \([-\pi,\pi]\), donde \(s_n(x)=\alpha_0/2+\sum_{k=1}^n \left( \alpha_k\cos(kx)+\beta_k\sen(kx) \right)\). Entonces \[ \begin{eqnarray*} \alpha_0&=&\frac{1}{\pi} \int_{-\pi}^{\pi} f(t)dt \\ \alpha_k&=&\frac{1}{\pi}\int_{-\pi}^{\pi} f(t)\cos(kt)dt \\ \beta_k&=&\frac{1}{\pi}\int_{-\pi}^{\pi} f(t)\sen(kt)dt \\ \end{eqnarray*} \] que son precisamente los coeficientes de Fourier de \(f\) con respecto al sistema trigonométrico básico.
Fijamos un entero \(m\geq 1\).
Por las propiedades de la convergencia uniforme con respecto a la integral tenemos \[ \int_{-\pi}^\pi f(x)\cos(mx)dx = \lim_{n\to \infty} \int_{-\pi}^{\pi}s_n(x)\cos(mx)dx, \] pero por las relaciones de ortogonalidad resulta que si \(n> m\) entonces \[ \begin{eqnarray*} \int_{-\pi}^{\pi} s_n(x)\cos(mx)dx&=&A\int_{-\pi}^{\pi}\cos(mx)dx \\ &+& \sum_{k=1}^n \alpha_k\int_{-\pi}^{\pi} \cos(kx)\cos(mx)dx \\ &+& \sum_{k=1}^n \beta_k\int_{-\pi}^{\pi} \sen(kx)\cos(mx)dx \\ &=& \alpha_m\int_{-\pi}^{\pi} \cos^2(mx)dx \\ &=& \alpha_m\pi \end{eqnarray*} \] y obtenemos \[ \begin{eqnarray*} \int_{-\pi}^\pi f(x)\cos(mx)dx=\lim_{n\to \infty} \int_{-\pi}^{\pi}s_n(x)\cos(mx)dx = \alpha_m \pi \end{eqnarray*} \] para concluir \[ \frac{1}{\pi}\int_{-\pi}^{\pi} f(x)\cos(mx)dx=\alpha_m. \] De manera similar se puede obtener que \[ \frac{1}{\pi}\int_{-\pi}^{\pi} f(x)\sen(mx)dx=\beta_m. \]
Para \(\alpha_0\) usando nuevamente la convergencia uniforme si integramos la serie \[ f(x)=\frac{\alpha_0}{2}+\sum_{k=1}^\infty \left( \alpha_k\cos(kt)+\beta_k\sen(kt) \right) \] término a término y usamos las relaciones de ortogonalidad llegamos a \[ \begin{eqnarray*} \int_{-\pi}^{\pi} f(x)dx&=&\frac{\alpha_0}{2} \int_{-\pi}^{\pi} 1 dx \\ &+& \sum_{k=1}^\infty \alpha_k\int_{-\pi}^{\pi}\cos(kx)dx \\ &+& \sum_{k=1}^\infty \beta_k\int_{-\pi}^{\pi}\sen(kx)dx \\ &=&\frac{\alpha_0}{2}(2\pi)\\ &=& \alpha_0 \pi \end{eqnarray*} \] y concluimos \[ \frac{1}{\pi}\int_{-\pi}^{\pi} f(x)dx=\alpha_0 \]
Definición
Sea \(f:\mathbb{R} \to \mathbb{R}\) una función de periodo \(2\pi\) integrable en \([-\pi,\pi]\). Definimos la serie de Fourier de \(f\), con respecto al sistema trigonométrico básico, como \[ a_0+\sum_{k=1}^{\infty}(a_k\cos(kx)+ b_k \sen(kx)) \] donde \(\{a_k\}_{k=0}^\infty \cup \{ b_k\}_{k=1}^\infty\) son los coeficientes de Fourier de \(f\).
Una de las aportaciones más importantes de Fourier es encontrar condiciones, sobre la función \(f\), para la cual se tenga \[ f(x)=a_0+\sum_{k=1}^{\infty}(a_k\cos(kx)+ b_k \sen(kx)) \] tanto convergencia puntual y/o uniforme.
Definición
Sea \(f:[a,b]\to \mathbb{R}\) una función tal que todas sus discontinuidades, de existir, son discontinuidades de salto. Por lo que los límites \(\lim_{x\to x_0^+}f(x)\) y \(\lim_{x\to x_0^-}f(x)\) siempre existe para todo \(x_0 \in [a,b] \). Denotamos \[ f(x_0^+)=\lim_{x\to x_0^+}f(x), \quad f(x_0^-)=\lim_{x\to x_0^-}f(x) \]
Dado \(x_0\in [a,b]\) definimos su derivada lateral derecha en \(x_0\) como \[ \lim_{h\to 0^+} \frac{f(x_0+h)-f(x_0^+)}{h} \] y su derivada lateral izquierda en \(x_0\) como \[ \lim_{h\to 0^-} \frac{f(x_0+h)-f(x_0^-)}{h} \] siempre y cuando los límites existan. Denotamos a estas derivadas como \(f'_+(x_0)\) y \(f'_-(x_0)\) respectivamente.
Teorema
Sea \(f\) una función de periodo \(2\pi\), tal que en un intervalo de longitud \(2\pi\) \(f\) tiene a lo más una cantidad finita de puntos de discontinuidad, todos ellos discontinuidades de salto.
Si \(f\) es continua en \(x\) y ambas derivadas laterales existen en \(x\) entonces \[ f(x)=\frac{a_0}{2}+\sum_{k=1}^\infty (a_k\cos(kx)+b_k\sen(kx)) \]
Si \(f\) es discontinua en \(x\) y ambas derivadas laterales existen en \(x\) entonces \[ \frac{f(x^+)+f(x^-)}{2}=\frac{a_0}{2}+\sum_{k=1}^\infty (a_k\cos(kx)+b_k\sen(kx)) \] Por último, si la función es continua en \([a,b]\) y ambas derivadas laterales existen en todo punto de \([a,b]\), la convergencia es uniforme en \([a,b]\).
Definición
Extensiones periódicas
Analizar funciones periódicas al principio parece algo restrictivo pero en realidad no lo es.
Supongamos que tenemos dada una función \(f:[-\pi,\pi]\to \mathbb{R}\) y queremos analizarla usando series de Fourier. No es periódica pero podemos extenderla a una función que sí lo sea (simplemente copiando su gráfica).
Caso 1
Tenemos que \(f(-\pi)=f(\pi)\). Entonces repitiendo los valores de \(f\) hacia la izquierda y derecha, en intervalos de longitud \(2\pi\) obtenmos una extensión de \(f\) a todo \(\mathbb{R}\) la cual es de periodo \(2\pi\).
Por ejemplo \(f(x)=x^2\), para \(x\in [-\pi,\pi]\). Su extensión se ve
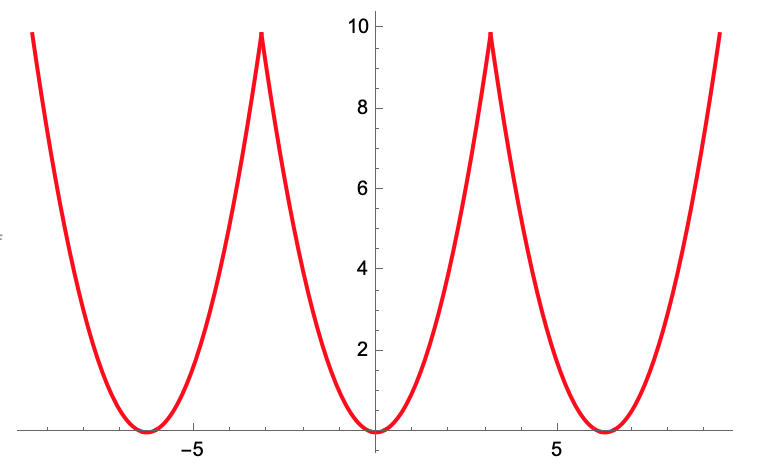
Caso 2
Si \(f(\pi)\ne f(\pi)\) tenemos que hacer algo diferente. En este caso podemos tomar dos caminos.
Primer método: extendenmos periódicamente la función \(f(x)\) pero sólo desde el intervalo \((-\pi,\pi)\), dejando los valores de la extensión indefinidos en todos los puntos de la forma \(x=k\pi\), \(k\in \mathbb{Z}\).
Segundo método: redefinimos la función \(f\) en alguno de los extremos \(x=-\pi\) ó \(x=\pi\) para que sean iguales y entonces tener el caso \(f(-\pi)=f(\pi)\).
Es imporante notar que en cualquiera de los dos métodos los coeficientes de Fourier de \(f\) no cambian pues sólo se modifica la función en un número finito de puntos por lo que el valor de la integral de Riemann no cambia.
Por ejemplo para \(f(x)=x\), \(x\in [-\pi,\pi]\), podemos redefinir \(f(x)=x\), para \(x\in (-\pi,\pi) \) y \(f(\pi+2\pi k)=-\pi\), para todo \(k\in \mathbb{Z}\). En este caso la extensión se ve
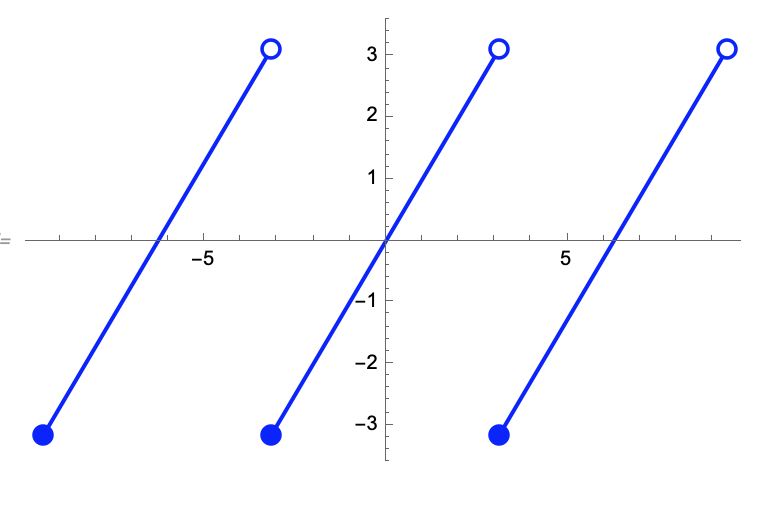
Ejercicio
Para la extensión periódica de \(f(x)=x^2\), en \(x\in [-\pi,\pi]\) encuentra:
- La serie de Fourier de \(f\).
- Usando el Teorema 7.16 , encuentra los puntos donde la serie de Fourier converge puntualmente a \(f\), los intervalos donde converge uniformemente a \(f\).
Ejercicio
Para la extensión periódica de la identidad, dada por \(f(x)=x\) en \(x\in (-\pi,\pi)\) y \(f(-\pi+2\pi k)=-\pi\), para toda \(k\in \mathbb{Z}\), encuentra:
- La serie de Fourier de \(f\).
- Usando el Teorema 7.16 , encuentra los puntos donde la serie de Fourier converge puntualmente a \(f\), los intervalos donde converge uniformemente a \(f\).
Ejercicio
Una función \(f\) se llama par si \(f(-x)=f(x)\) para todo \(x\) en el dominio de la función. Es decir, si su gráfica es simétrica con respecto el eje \(y\).
Una función \(f\) se llama impar si \(f(-x)=-f(x)\) para todo \(x\) en el dominio de la función. Es decir, si su gráfica es simétrica con respecto al origen.
Nota: en ambos casos se asume que el dominio de la función tiene la propiedad de que si \(x\) está entonces \(-x\) también (es decir, es simétrico con respecto al origen).
-
Prueba que:
- la multiplicación de dos funciones pares, o dos funciones impares, es par.
- la múltiplicación de una función par con una impar es impar.
- Si \(f\) es una función impar entonces \(f(0)=0\).
- Si \(f:[-a,a]\to \mathbb{R}\) es impar e integrable entonces \[ \int_{-a}^a f(t)dt=0. \]
- Si \(f:[-a,a]\to \mathbb{R}\) es par e integrable entonces \[ \int_{-a}^a f(t)dt=2\int_0^a f(t)dt. \]
- Concluye que si \(f\) es una función par entonces los coeficientes de Fourier de \(f\) satisfacen \[ b_k=0, a_k = \frac{2}{\pi}\int_0^{\pi}f(t)\cos(k t)dt \] para todo \(k\in \mathbb{N}\) y por lo tanto la serie de Fourier de \(f\) se ve \[ \frac{a_0}{2}+\sum_{k=1}^\infty a_k \cos(kx) \]
- Concluye que si \(f\) es una función impar entonces los coeficientes de Fourier de \(f\) satisfacen \[ a_k=0, b_k = \frac{2}{\pi}\int_0^{\pi}f(t)\sen(k t)dt \] para todo \(k\in \mathbb{N}\) y por lo tanto la serie de Fourier de \(f\) se ve \[ \sum_{k=1}^\infty b_k \sin(kx) \]
Ejercicio
Para la extensión periódica de \(f(x)=x^2\) en \(x\in (0,2\pi)\), encuentra:
- La serie de Fourier de \(f\).
- Usando el Teorema 7.16 , encuentra los puntos donde la serie de Fourier converge puntualmente a \(f\), los intervalos donde converge uniformemente a \(f\).
Ejercicio
Para la extensión periódica de la identidad, dada por \(f(x)=x\) en \(x\in (0,2\pi)\), encuentra:
- La serie de Fourier de \(f\).
- Usando el Teorema 7.16 , encuentra los puntos donde la serie de Fourier converge puntualmente a \(f\), los intervalos donde converge uniformemente a \(f\).
Ejercicio
Para la extensión periódica de cada una de las siguientes funciones, encuentra:
- La serie de Fourier de \(f\).
- Usando el Teorema 7.16 , encuentra los puntos donde la serie de Fourier converge puntualmente a \(f\), los intervalos donde converge uniformemente a \(f\).
- \(f(x)=e^{cx}\), donde \(x\in (-\pi,\pi)\) y \(c\) es una consante distinta de cero.
- \(f(x)=\cos(c x)\), donde \(x\in (-\pi,\pi)\) y \(c\) es una consante distinta de cero.
- \(f(x)=\sen(c x)\), donde \(x\in (-\pi,\pi)\) y \(c\) es una consante distinta de cero.
Ejercicio
Encuentra las series de Fourier de las extensiones periódicas de las siguientes funciones.
- Coseno hiperbólico \[ \frac{e^x+e^{-x}}{2}, \quad x\in (-\pi,\pi). \]
- Seno hiperbólico \[ \frac{e^x-e^{-x}}{2}, \quad x\in (-\pi,\pi). \]
Ejercicio
Sea \(f:\mathbb{R}\to \mathbb{R}\) una función integrable de periodo \(2\pi\). Asume que \(f\) es Lipschitz de orden \(\alpha >0\), es decir existe una constante \(M>0\) tal que \[ |f(x)-f(y)|\leq M |x-y|^\alpha \] para todos \(x,y\in \mathbb{R}\).
Prueba que los coeficientes de Fourier de \(f\) satisfacen \[ |a_n|\leq \frac{M\pi^\alpha}{n^\alpha} \quad |b_n|\leq \frac{M\pi^\alpha}{n^\alpha} \]
Concluye que para \(\alpha > 1\) la serie de Fourier de \(f\) converge absolutamente y uniformemente en todo \(\mathbb{R}\).
Ejercicio
Sea \(f:\mathbb{R}\to \mathbb{R}\) una función integrable de periodo \(2\pi\) con serie de Fourier \[ \frac{a_0}{2}+\sum_{k=1}^\infty (a_k \cos(kx)+ b_k\sen(kx)) \]
Define \[ f_i(x)=\frac{f(x)-f(-x)}{2}, \quad f_p(x)=\frac{f(x)+f(-x)}{2} \]
- Prueba que \(f_i\) es una función impar de periodo \(2\pi\) con serie de Fourier \[ \sum_{k=1}^\infty b_k\sen(kx). \]
- Prueba que \(f_p\) es una función par de periodo \(2\pi\) con serie de Fourier \[ \frac{a_0}{2}+\sum_{k=1}^\infty a_k \cos(kx). \]
- Prueba que la serie de Fourier de \(f(x-\pi)\) es \[ \frac{a_0}{2}+\sum_{k=1}^\infty (-1)^k (a_k\cos(kx)+ b_k\sen(kx)). \]