Topología en espacios métricos

Introducción

La topología se refiere a la parte de las matemáticas que estudia la expansión del concepto de continuidad más allá de los espacios \(\mathbb{R}^n\) o los espacios métricos. La idea principal detrás de dicha generalización es que existen ciertos subconjuntos con características especiales que permiten definir los conceptos de continuidad. A estos subconjuntos especiales se les llama subconjuntos abiertos e intuitivamente son los que "miden" la cercanía entre puntos de un espacio dado.

En esta sección se introducen los conceptos de conjuntos abiertos y cerrados en espacios métricos, se ven sus propidades básicas así como algunos ejemplos concretos en los espacios \(\mathbb{R}^n\) y \(\mathcal{B}(X)\), el espacio de funciones acotadas.

Definición

Sea \((X,d)\) un espacio métrico. Una bola abierta de radio \(r>0\) y centrada en \(x_0\in X\) se define como el conjunto \[ B_r(x_0)=\{ x\in X: d(x,x_0)< r\}. \] Si el espacio métrico proviene de un espacio vectorial normado \((V,\|\cdot \|)\) las bolas son \[ B_r(x_0)=\{ x\in V: \| x-x_0\| < r\}. \]

Además es últil observar que, gracias a la estructura de espacio vectorial, podemos expresar \[ B_r(x_0)=x_0+B_r(0) \] por lo que en espacios vectoriales normados las bolas con centro en origen juegan un papel primordial.

La forma de la bola depende del espacio métrico, como se ven en los siguientes ejemplos.

La métrica discreta.

Recordamos que, para un conjunto cualquiera \(X\ne \emptyset\), la métrica discreta en \(X\) de se define por \[ d(x,y)=\left\{\begin{array}{cc} 0 & \textrm{si \(x=y\)} \\ 1 & \textrm{si \(x\ne y\)} \end{array} \right. \]

Con la métrica discreta se tiene que para todo radio \(r\in (0,1]\): \[ B_r(x_0)=\{x_0\}, \] y para todo \(r\in (1,\infty)\): \[ B_r(x_0)=X. \]
Las normas-\(p\).

En el espacio vectorial normado \((\mathbb{R}^n, \|\cdot\|_p)\), con \(p\in [1,\infty]\), al forma de la bola depende del parámetro \(p\). La figura de abajo muestra algunas bolas en \(\mathbb{R}^2\), centradas en el origen.
La norma uniforme o infinito.

Sea \(X\ne\emptyset\) un conjunto cualquiera y considera el espacio vectorial normado de las funciones con valores reales, acotadas en \(X\) y con la norma uniforme (ó norma infinito), denotado \((\mathcal{B}(X),\|\cdot\|_\infty)\).

Dibujar bolas abiertas en \((\mathcal{B}(X), \| \cdot\|_\infty)\) no es tan directo pero tenemos cierta ayuda visual. En este caso una bola abierta es \[ B_r(f_0)=\{ f\in \mathcal{B}(X): \|f-f_0\|_\infty < r\} \] donde \(f,f_0\) son funciones acotadas sobre \(X\) con valores reales. En el análisis de los límites en la norma uniforme notamos que la expresión \(\|f-f_0\|< r\) implica \[ |f(x)-f_0(x)|< r, \quad \textrm{para toda \(x\in X\)} \] En términos de las gráficas de \(f\) y \(f_0\) quiere decir que la gráfica de \(f\) está encerrada en una franja de radio \(r>0\) centrada en \(f_0\). Por lo tanto podemos "dibujar" las bolas \(B_r(f_0)\) como

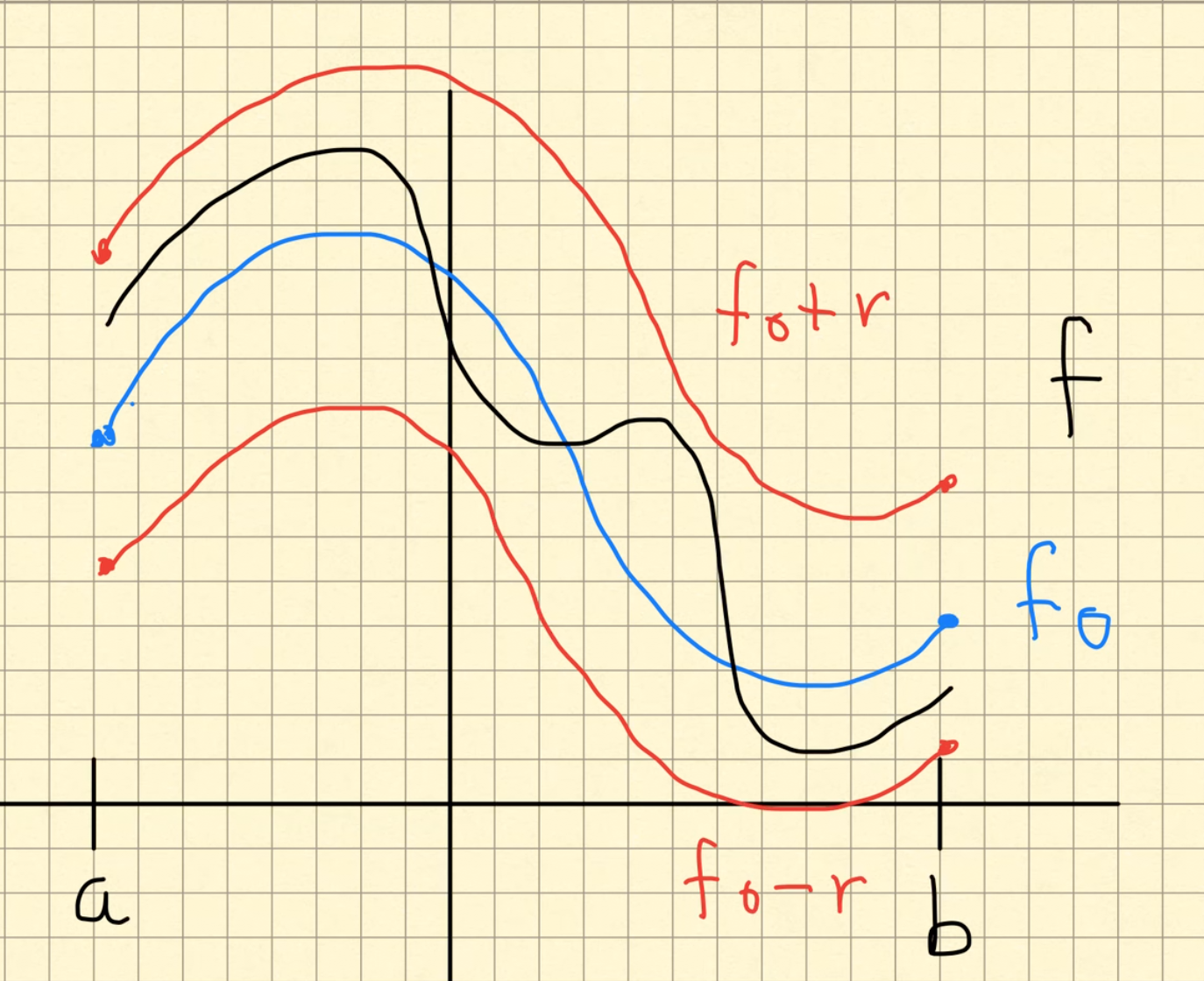
Definición

Sea \((X,d)\) un espacio métrico. Decimos que un subconjunto \(U\subseteq X\) es abierto en \((X,d)\) si todo punto de \(U\) admite una bola centrada en el punto contenida en \(U\), es decir:

para todo \(x\in U\) existe \(r>0\) tal que \(B_r(x)\subseteq U\).

Notas.

Dado \(x\in U\) el radio \(r\) que cumple \(B_r(x) \subseteq U\) usualmente depende de \(x\).
El cuantificador "para todo" es muy importante. Si existe un sólo punto \(x\in U\) para el cual no se puede encontrar \(r>0\) que satisfaga \(B_r(x)\subseteq U\), entonces el conjunto no es abierto.

Por ejemplo, en \((\mathbb{R}, |\cdot|)\) los intervalos de la forma \((a,b)\) son subconjuntos abiertos pues para cualquier \(x\in (a,b)\), si tomamos \(r=\min\{x-a, b-x\}\), entonces \(B_r(x)\subset (a,b)\).

Sin embargo el intervalo \((a,b]\) no es abierto pues, para el elemento \(b\in (a,b]\), siempre se tiene que, sin importar que radio \(r>0\) se tome, \(B_r(b)\cap (a,b]^c \ne \emptyset\), por lo que \(B_r(b)\) no puede estar contenido en \((a,b]\). Nota: \((a,b]^c\) denota el complemento de \((a,b]\)

Hay dos conjuntos especiales, en cualquier espacio métrico \((X,d)\), que siempre son abiertos. Estos son \(\emptyset\) y \(X\) (el vacío y el total). Sin embargo, para cualquier otro conjunto la métrica \(d\) "decide" si es abierto o no.

Lema

A pesar de que llamamos "bolas abiertas" a los conjuntos \[ B_r(x_0)=\{x\in X: d(x,x_0)< r\} \] formalmente debemos de usar la Definicion 5.3 para probar que son subconjuntos abiertos.

Sea \((X,d)\) un espacio métrico. Toda bola abierta es un subconjunto abierto de \(X\).

Proposición

Sea \((X,d)\) un espacio métrico.

Sea \(\{U_i\}_{i\in I}\) una colección arbitraria de conjuntos abiertos. Prueba que la unión \(\cup_{i\in I}U_i\), es abierta.
Sea \(U_1,\dots, U_n\) una colección finita de conjuntos abiertos. Prueba que la intersección \(\cap_{i=1}^n U_i\) es abierta.
Da un ejemplo de un espacio métrico y una colección numerable de conjuntos abiertos, \(\{U_i\}_{i\in \mathbb{N}}\), tal que su intersección \(\cap_{i\in \mathbb{N}} U_i\) no es abierta.

Sea \(x \in \cup_{i \in I} U_i\), entonces existe \(j \in I\) tal que \(x \in U_j\). Como \(U_j\) es abierto y \(x \in U_j\) entonces existe \(r>0\) tal que \(B_r(x) \subseteq U_j \subseteq \cup_{i \in I}U_i\).
Sea \(x \in \cap_{i=1}^n U_i\), entonces \(x \in U_j\) para \(j=1,...,n\) y existen \(r_1, ...,r_n > 0\) tales que \(B_{r_j}(x) \subseteq U_j\) para cada \(j=1,...,n\). Sea \(r=\min\{r_1,...,r_n\}\), entonces \(B_r(x) \subseteq U_j\) para cada \(j\) y \(B_r(x) \subseteq \cap_{i=1}^n U_i\).
Trabajaremos en \(\mathbb{R}\) con la métrica usual, \(d(x,y)=|y-x|\) y consideremos la colección de abiertos \(U_i = (\frac{-1}{i},\frac{1}{i})\). Afirmamos que \(\cap_{i \in \mathbb{N}} U_i = \{0\}\) y que dicho conjunto no es abierto en \(\mathbb{R}\). Como \(0 \in \frac{-1}{i},\frac{1}{i})\) para cada \(i\), entonces \(0 \in \cap U_i\). Si \(x>0\) entonces existe \(n \in \mathbb{N}\) tal que \(1/n < x\), por lo que \(x \notin (\frac{-1}{n},\frac{1}{n})\) y tampoco pertenece a la intersección. El resultado es análogo si suponemos que \(x < 0\). Para terminar basta notar que \(\{0\}\) es un conjunto finito y que toda bola abierta en \(\mathbb{R}\) es infinita, por lo que \(\cap_{i \in \mathbb{N}}U_i\) no es un conjunto abierto.

Ejercicio

Sea \((X,d)\) un espacio métrico y \(U\subseteq X\). Las siguientes condiciones son equivalentes.

\(U\) es abierto.
Si \((x_n)_{n\in \mathbb{N}} \subset X\) es una sucesión convergente a un punto \(x\in U \), entonces, \(x_n \in U\) para todos los \(x_n\)'s excepto un número finito.

Definicion

Sea \((X,d)\) un espacio métrico. Un subconjunto \(F\subset X\) se llama cerrado si su complemento \(F^c=X\setminus F\) es abierto.

Por ejemplo, en \((\mathbb{R},|\cdot|)\), el intervalo \([a,b]\) es un subconjunto cerrado pues su complemente \[ [a,b]^c=(-\infty,a)\cup (b,\infty) \] es abierto, al ser la unión de los abiertos \[ (-\infty,a )\cup (b,\infty)=\cup_{i=1}^\infty (a-i,a)\cup \cup_{j=1}^\infty (b,b+j) \]

Otro ejemplo es \(\mathbb{N}\) el cual es cerrado en \(\mathbb{R}\).

También notamos que en cualquier espacio métrico \((X,d)\) tanto \(\emptyset\) como \(X\) son subconjuntos cerrados.

Proposición

Sea \((X,d)\) un espacio métrico.

Sea \(\{F_i\}_{i\in I}\) una colección arbitraria de conjuntos cerrados. Prueba que la intersección \(\cap_{i\in I}F_i\), es cerrada.
Sea \(F_1,\dots, F_n\) una colección finita de conjuntos cerrados. Prueba que la union \(\cup_{i=1}^n F_i\) es cerrada.
Da un ejemplo de un espacio métrico y una colección numerable de conjuntos cerrados, \(\{F_i\}_{i\in \mathbb{N}}\), tal que su union \(\cup_{i\in \mathbb{N}} F_i\) no es cerrada.

Ejercicio

Sea \((X,d)\) un espacio métrico. Prueba que todo subconjunto finito de \(X\) es cerrado.

Ejercicio

Sea \((X,d)\) un espacio métrico, \(F\subseteq X\) un conjunto cerrado y \(U \subseteq X\) un conjunto abierto.

Prueba que \(F\setminus U\) es cerrado y que \(U \setminus F \) es abierto.

Ejercicio

En el Ejercicio 5.15 se definió que dos métricas son equivalentes si tienen las mismas sucesiones convergentes.

Prueba que dos métricas son equivalentes si y sólo si generan los mismos conjuntos abiertos.

Definición

Sea \((X,d)\) un espacio métrico y \(A\subseteq X\).

Un punto \(x\in X\) se llama punto interior de \(A\) si existe un \(r>0\) tal que \(B_r(x)\subseteq A\).
Un punto \(x\in X\) se llama punto de acumulación o punto límite de \(A\) si para todo \(n\in \mathbb{N}\) existe un \(a_n\in A\) tal que \(0< d(a_n,x) \leq \frac{1}{n}\). Observación: ya que pedimos \(0< d(a_n,x)\) necesariamente se tiene que \(a_n\ne x\).

Teorema

Sea \((X,d)\) un espacio métrico y \( A \subseteq X\). Las siguientes condiciones son equivalentes:

\(A\) es abierto.
Todo punto de \(A\) es un punto interior de \(A\).

Teorema

Sea \((X,d)\) un espacio métrico y \(B \subseteq X\). Las siguientes condiciones son equivalentes:

\(B \) es cerrado.
\(B\) contiene a todos sus puntos de acumulación.

Ejercicio

Considera el espacio métrico \((\mathbb{R},|\cdot|)\).

Prueba que \(\mathbb{Q}\) no es ni abierto ni cerrado en \(\mathbb{R}\).
¿Existe un conjunto abierto en \(\mathbb{R}\), no vacío, contenido en \(\mathbb{Q}\)?
Da un ejemplo de un subconjunto de \(\mathbb{R}\), cerrado y que consiste sólo de números irracionales.

Ejercicio

Prueba que todo intervalo abierto de \(\mathbb{R}\) es la unión numerable de intervalos cerrados.
Prueba que todo intervalo cerrado de \(\mathbb{R}\) es la intersección numerable de intervalos abiertos.

Ejercicio

Sea \((X,d_X)\), \((Y,d_Y)\) dos espacios métricos y \(A \subseteq X\), \(B\subseteq Y\). Cosdiera el espacio métrico \(X\times Y, d\) con la métrica \[ \sigma((x_1,y_1),(x_2,y_2))= \sqrt{d_X(x_1,x_2)^2+d_Y(y_1,y_2)^2} \] Ver Ejercicio 4.22.

Si \(A\) es abierto en \(X\) y \(B\) es abierto en \(Y\) prueba que \(A\times B\) es abierto en \(X\times Y\).
Si \(A\) es cerrado en \(X\) y \(B\) es cerrado en \(Y\) prueba que \(A\times B\) es cerrado en \(X\times Y\).

Nota: gracias al Ejercicio 5.14 y Ejercicio 6.11, éste ejercicio sigue siendo válidos si se reemplaza \(\sigma\) por cualquier otra de las métricas del Ejercicio 4.22.

Definición

Sean \((X,d_Y)\) y \((Y,d_Y)\) dos espacios métricos.

Ya que todas las métricas \begin{eqnarray*} d((x_1,y_1),(x_2,y_2))&=& d_X(x_1,x_2)+d_Y(y_1,y_2),\\ \rho((x_1,y_1),(x_2,y_2)) &=& \max\{d_X(x_1,x_2), d_Y(y_1,y_2) \}\\ \sigma((x_1,y_1),(x_2,y_2)) &=& \sqrt{d_X(x_1,x_2)^2+d_Y(y_1,y_2)^2}. \end{eqnarray*} son equivalentes (gracias al Ejercicio 5.14) van a generar los mismos subconjuntos abiertos en \(X\times Y\), (ver Ejercicio 6.11). Por lo tanto definimos el producto de los espacios métricos \((X,d_X)\) y \((Y,d_Y)\) como el espacio métrico \(X\times Y\) dotado con cualquiera de las métricas anteriores.

Ejercicio

Para \(k\in \mathbb{N}\) denota \(e^{(k)}\) la sucesión de números reales que es todo cero excepto en el lugar \(k\), donde tiene un 1. Prueba que el conjunto \(\{e^{(k)}\}_{k\in \mathbb{N}}\) es cerrado en \((\ell_p, \|\cdot\|_p)\), para todo \(p\in [1,\infty]\).

Sugerencia: primero prueba que \(\{e^{(k)}\}_{k\in \mathbb{N}}\) no tiene puntos de acumulación y luego usa el Teorema 6.14.

Ejercicio

Considera el espacio vectorial normado \((\ell_\infty, \|\cdot\|_\infty)\). Por \(c_0\) denotamos al conjunto de sucesiones de números reales que convergen a cero. Ya que toda sucesión convergente es acotada tenemos que \(c_0 \subseteq \ell_\infty\).

Prueba que \(c_0\) es cerrado en \(\ell_\infty\).

Definición

Sea \((X,d)\) un espacio métrico y \(A \subseteq X\).

Se define el interior de \(A\), denotado \(\inte(A)\) ó \(A^o\) como \[ \inte(A)=\cup\{ U \subseteq X : \textrm{\(U\) es abierto en \(X\) y \(U \subseteq A\)}\} \]

Ya que siempre tenemos \(\emptyset \subset A\) y \(\emptyset\) es un conjunto abierto, el interior de un conjunto está bien definido. Además, usando que unión arbitraria de conjuntos abiertos es abierta (Ejercicio 6.5) resulta que el interior de un conjunto siempre es un conjunto abierto. Finalmente, como el interior es la unión de todos los abiertos contenidos en el conjunto también es el abierto más grande contenido en el conjunto.

Se define la cerradura de \(A\), denotada \(\cer(A)\) ó \(\overline{A}\) como el cerrado más chico que contiene a \(A\), es decir \[ \cer(A)=\cap \{ F\subseteq X: \textrm{\(F\) es cerrado en \(X\) y \(A\subseteq F\)} \} \] Ya que \(X\) es un conjunto cerrado y \(A\subset X\) la cerradura está bien definida. Además por el Ejercicio 6.8 tenemos que \(\cer(A)\) es siempre un conjunto cerrado.

Nota que si \(A\) es cerrado entonces \(A=\overline{A}\) y si \(A\) es abierto \(\inte(A)=A\).

Lema

Sea \((X,d)\) un espacio métrico y \(A\subseteq X\).

Un punto \(x\in X\) satisface \(x\in \overline{A}\) si y sólo si para toda \(r>0\), \(B_r(x)\cap A \ne \emptyset\).

Un punto \(x\in X\) satisface \(x\in A^o\) si y sólo si exite \(r>0\) tal que \(B_r(x)\subseteq A \).

Lema

Sea \((X,d)\) un espacio métrico y \(A\subseteq X\).

Prueba que \(x\in \overline{A}\) si y sólo si existe una sucesión de elementos de \(A\), \((a_n)_{n\in \mathbb{N}} \subset A\), tal que \(\lim_na_n=x\).

Ejercicio

Prueba las siguientes indentidades.

\(\inte([a,b) )= (a,b)\), \(\cer([a,b))=[a,b]\).
\(\inte(\mathbb{Q})=\emptyset\), \(\cer(\mathbb{Q})=\mathbb{R}\) .
\(\inte(\Delta)=\emptyset\), \(\cer(\Delta)=\Delta\), donde \(\Delta\) es el conjunto de cantor.

Ejercicio

Sea \((X,d)\) un espacio métrico y \(A,B \subseteq X\).

Prueba \(\cer(A\cup B)=\cer(A)\cup \cer(B)\).
Prueba \(\cer(A \cap B)\subseteq \cer(A)\cap \cer(B) \) y da un ejemplo que muestre que la contención puede ser propia.
Prueba \(\inte(A\cap B)= \inte(A)\cap \inte(B)\).
Prueba \(\inte(A)\cup \inte(B) \subseteq \inte(A\cup B) \) y da un ejemplo que muestre que la contención puede ser propia.

Ejercicio

Sea \((X,d)\) un espacio métrico y \(A\subseteq X\).

Si \(x\in X\) es un punto límite de \(A\) prueba que para todo abierto \(U\) tal que \(x\in U\) contiene una cantidad infinita de elementos de \(A\).

Ejercicio

Sea \((X,d)\) un espacio métrico, \(A\subseteq X\) y \(x\in X\).

Prueba que \(x\) es un punto límite de \(A\) si y sólo si existe una sucesión \((a_n)_{n\in \mathbb{N}} \subset A\) tal que \(\lim_{n\to \infty}a_n=x\) y \(a_n\neq x\), para toda \(n\).

Ejercicio

Sea \((X,d)\) un espacio métrico y \(A\subseteq X\). Por \(A'\) denotamos al conjunto de todolos puntos de acumulación de \(A\).

Prueba que \(A'\) es un conjunto cerrado.
Prueba que \(\overline{A}=A\cup A'\).

Ejercicio

Sea \((X,d)\) un espacio métrico y \(A \subseteq X\). Un punto \(x\in X\) se llama punto frontera de \(A\) si, para todo \(r>0\) se cumple \[ B_r(x)\cap A \ne \emptyset \quad \textrm{y} \quad B_r(x)\cap A^c \ne \emptyset. \] Al conjunto de puntos frontera lo denotamos por \(\partial(A)\).

Prueba las siguientes identidades.

\(\partial(A)=\partial(A^c)\).
\(\overline{A}=\inte(A)\cup \partial(A)\).
\(X= \inte(A)\cup \partial(A)\cup \inte(A^c)\).

Ejercicio

Sea \((X,d)\) un espacio métrico, \(x_0\in X\) y \(r>0\). El conjunto \[ \{x\in X: d(x,x_0) \leq r\} \] se llama la bola cerrada, centrada en \(x\), de radio \(r\).

Prueba que la bola cerrada es un subconjunto cerrado pero da un ejemplo que muestra que la cerradura de la bola abierta no es la bola cerrada, es decir: \[ \overline{B_r(x_0)} \ne \{x\in X: d(x,x_0) \leq r\} \]

Sugerencia: metrica discreta.

Ejercicio

Sea \((V,\|\cdot\|)\) un espacio vectorial normado, \(v_0\in V\), \(r>0\).

Prueba \[ \overline{B_r(v_0)}=\{ v\in V: \| v-v_0\| \leq r\}. \]

Es decir, para espacios vectoriales normados la cerradura de la bola abierta sí es la bola cerrada.

Lema

Sea \((X,d)\) un espacio métrico y \(A\subseteq X\). Prueba que \(\operatorname{diam}(A)=\operatorname{diam}(\overline{A})\).

Ver Ejercicio 2.26 para definción de diámetro.

Recordemos que en la sección anterior demostramos que si \(\lim_{n \to \infty} x_n = x\) y \(\lim_{n \to \infty} y_n = y\) entonces \(d(x,y)= \lim_{n \to \infty} d(x_n,y_n)\), asimismo \(z \in \overline{A}\) si y sólo si existe una sucesión \((z_n)_{n \in \mathbb{N}} \subseteq A\) que converge a \(z\). Sean \(a,b \in \overline{A}\) y \((a_n), (b_n)\) sucesiones en \(A\) tales que \(\lim a_n = a\) y \(\lim b_n = b\). Para cada \(n \in \mathbb{N}\) se tiene que \(d(a_n,b_n) \leq \operatorname{diam}(A)\), por lo que \(d(a,b) = \lim_{n \to \infty} d(a_n,b_n) \leq \operatorname{diam}(A)\). En consecuencia \(\operatorname{diam}(\overline{A}) = \sup_{a,b \in \overline A} d(a,b) \leq \operatorname{diam}(A)\)
La otra contención es consecuencia de las propiedades del supremo, como \(A \subseteq \overline A\) entonces \(\sup_{a,b \in A}\{d(a,b)\} \leq \sup_{a,b \in \overline A}d(a,b)\) y \(\operatorname{diam}(A) \leq \operatorname{diam}(\overline A)\).

Lema

Sea \((X,d)\) un espacio métrico y \(A\subseteq X\) un subconjunto no vacío. Dado un punto \(x\in X\) se define la distancia de \(x\) al subconjunto \(A\) como \[ d(x,A)=\inf\{d(x,a): a\in A \}. \]

Prueba que \(x\in \overline{A}\) si y sólo si \(d(x,A)=0\).

Sugerencia: Ejercicio 5.21

Ejercicio

Sea \((X,d_X)\) un espacio métrico. Decimos que un subconjunto \( D \subseteq X\) se llama denso en \(X\) si \(\overline{D}=X\). Por ejemplo \(\mathbb{Q}\) es denso en \(\mathbb{R}\).

Prueba que las siguientes condiciones son equivalentes.

\(D\) es denso en \(X\).
Para todo \(x\in X\) existe una sucesión de elementos de \(D\), \((d_n)_{n=1}^\infty \subseteq D\), tal que \(\lim_{n\to \infty} d_n=x\).
Para todo \(x\in X\) y para toda \(r>0\), \(B_r(x)\cap D \ne \emptyset \).
Para todo subconjunto abierto no vacío \(U \subseteq X\), \(U\cap D \ne \emptyset\).
\(D^c\) tiene interior vacío.

Quiz

(2 pts) Sean \(\alpha\) un real fijo y \(y \in \mathbb{R}^n\) un vector fijo. Considera el subconjunto \[ F=\{x\in \mathbb{R}^n: x\cdot y \geq \alpha\} \] donde \(x\cdot y\) denota el producto punto en \(\mathbb{R}^n\). Prueba que \(F\) es un subconjunto cerrado.
(3 pts) Sea \((V,\|\cdot\|)\) un espacio vectorial normado y \(U\subseteq V\) un subconjunto abierto. Toma un escalar fijo \(\alpha \ne 0\) y define \[ W=\{\alpha u: u\in U\} \] es decir, \(W\) es la homotecia de \(U\) bajo \(\alpha\). Prueba que \(W\) es un subconjunto abierto.