El axioma del supremo
Introducción
El axioma del supremo es lo que hace a los reales los reales. Por ejemplo, los números racionales satisfacen todos los axiomas de campo y de orden de la sección anterior, sin embargo, el cálculo diferencial e integral usa a los números reales por que en éstos se puede asegurar (entre otras muchas cosas): la solución a un gran número de ecuaciones algebráicas, la convergencia de límites y series, la existencia de derivadas. Otras palabras que se usan para expresar lo anterior es que los números reales son completos, lo que se pueden pensar como que la recta real no tiene hoyos. Esta seccíon es muy importante pues trata al axioma del supremo, sus propiedades y consecuencias.
Definición
Un conjunto no vacío \(A \subseteq \mathbb{R}\) se llama:- acotado superiormente si existe \(M\) tal que \(a \leq M\), para toda \(a\in A\).
- acotado inferiormente si existe \(m\) tal que \(m \leq a\), para toda \(a\in A\).
Ejercicio
Sea \(m>0\) y \(a,b\in \mathbb{R}\).- Demuestra que el intervalo solución de \(\{ x: mx+b \leq a \}\) siempre está acotado superiormente.
- Demuestra que el intervalo solución de \(\{x: x^2-3mx+2m^2 \leq 6m^2\}\) está acotado superior e inferiormente.
Ejercicio
Fija \(a>0\) y define \(S=\{ x \geq 0: x^2 \leq a \}\). Demuestra que \(A\) está cotado superiormente.
Sugerencia: primero, usa el Ejercicio 1.27 para notar \(a<(1+a)^2\); después, para \(x\in S\), prueba \(0< (1+a)^2-x^2\); finalmente, usa diferencia de cuadrados para probar \(x< 1+a\), para toda \(x\in S\).
Definición
El supremo de un conjunto \(S\) es la cota superior más chica. Es decir, \(\alpha\) es el supremo de \(S\) si satisface:
- \(x \leq \alpha\), para todo \(x\in S\);
- si \(M\) satisface \( x \leq M \), para todo \(x\in S\) entonces \(\alpha \leq M \).
El ínfimo de un conjunto \(S\) es la cota inferior más grande. Es decir, \(\alpha\) es el ínfimo de \(S\) si satisface:
- \(\alpha \leq x\), para todo \(x\in S\);
- si \(m\) satisface \( m \leq x \), para todo \(x\in S\) entonces \(m \leq \alpha\).
Notación: por \(\sup(A)\), \(\inf(A)\), denotamos el supremo e ínfimo del conjunto \(A\), respectivamente (siempre que éstos existan).
Proposición
El supremo de un conjunto (de existir) es único, es decir, demuestra que si \(\alpha\) y \(\beta\) son dos números que satisfacen las dos condiciones de la definición del supremo entonces \(\alpha=\beta\).
El ínfimo de un conjunto (de existir) es único, es decir, demuestra que si \(\alpha\) y \(\beta\) son dos números que satisfacen las dos condiciones de la definición del ínfimo entonces \(\alpha=\beta\).
Proposición
Caracterización del supremo.
Demuestra que \(\alpha\) es el supremo de \(S\) si y sólo si \(\alpha\) satisface:
- \(\alpha\) es cota superior de \(S\);
- para todo \(\varepsilon>0\), exsite \(x_0 \in S\) tal que \(\alpha- \varepsilon < x_0\).
Caracterización del ínfimo.
Demuestra que \(\alpha\) es el ínfimo de \(S\) si y sólo si \(\alpha\) satisface:
- \(\alpha\) es cota inferior de \(S\);
- para todo \(\varepsilon>0\), exsite \(x_0 \in S\) tal que \(\alpha + \varepsilon > x_0\).
Axioma del supremo
Todo subconjunto no vacío de reales, acotado superiormente tiene supremo.
Nota: una vez que se estipula el axioma del supremo, no es necesario estipular el axioma del ínfimo, pues a partir del axioma del supremo se puede probar la siguiente propiedad (que sería el enunciado del axioma del ínfimo)
Todo subconjunto no vacío de reales, acotado inferiormente tiene un ínfimo.
Ver Ejercicio 3.14 más adelante.
Teorema.
El principio Arquimideano
Sea \(x>0\) fijo y arbitrario. Demuestra que existe un natural \(n\) que satisface \(x< n\).
Sugerencia: usa la proposición anterior.
Ejercicio
Sea \(x>0\) fijo y arbitrario. Demuestra que existe un natural que satisface \(\frac{1}{n}< x\).Sugerencia: aplica la propiedad Arquimideana a \(\frac{1}{x}\).
Proposición
Densidad de los racionales
Sean \(x,y\in \mathbb{R}\) con \(x< y\). Prueba que existe \(r\in \mathbb{Q}\) tal que \(x< r < y\).
Por el ejercicio anterior existe un \(n_0\in \mathbb{N}\) tal que \(\frac{1}{n_0}< y-x\). Por la propiedad Arquimideana, aplicada a \(\frac{1}{n_0}\) y \(x\), existe un \(k \in \mathbb{N}\) tal que \(x< \frac{k}{n_0}\). Definimos \[ S=\left\{ m \in \mathbb{N}: x< \frac{m}{n_0} \right\}. \] Por lo anterior \(k \in S\) así que \(S\ne \emptyset\) por lo tanto podemos aplicar el principio del buen orden de los naturales y podemos encontrar \(m_0=\min(S)\). Se sigue que \(x< \frac{m_0}{n_0}\).
Afirmamos que también se cumple \(\frac{m_0}{n_0} < y\). De no ser así \(\frac{m_0}{n_0} \geq y\). Además como \(m_0\) es el mínimo de \(S\), \(m_0-1\notin S\) por lo que \(\frac{m_0-1}{n_0} \leq x\). Sumando las desigualdades \begin{eqnarray*} \frac{m_0}{n_0} & \geq & y \\ -\frac{m_0-1}{n_0} & \geq & - x \end{eqnarray*} obtenemos \[ \frac{1}{n_0}= \frac{m_0}{n_0} -\frac{m_0-1}{n_0} \geq y - x \] contradiciendo la desigualdad \( \frac{1}{n_0} < y- x\).
Ejercicio
Considera el conjunto
\[ A=\left\{ \frac{1}{n}: n=1,2,\dots \right\} \] Demuestra que \(\inf(A)=0\). Sugerencia: usa el Ejercicio 3.11.
Ejercicio
Considera dos conjuntos no vacios, \(A,B \subseteq \mathbb{R}\) y supon que \(A \subseteq B\). Demuestra:
- Si \(B\) está acotado superiormente también \(A\) y \(\sup(A) \leq \sup(B)\).
- Si \(B\) está acotado inferiormente también \(A\) y \(\inf(B)\leq \inf(A).\)
Ejercicio
Sea \(\emptyset \ne A \subseteq \mathbb{R}\). Define
\[ B=\{-a: a\in A\}. \]Demuestra que si \(A\) está acotado superiormente si y sólo si \(B\) está acotado inferiormente y que
\[ \inf(B)=-\sup(A). \]Usa lo anterior junto con el axioma del supremo para probar que todo subconjunto no vacío y acotado inferiormente de \(\mathbb{R}\) admite ínfimo.
Proposición
Sea \(\emptyset \ne A \subseteq \mathbb{R}\) y sean \(\gamma \in \mathbb{R}\) y \(\beta \in \mathbb{R}^+\), fijos y arbitrarios. Define el siguiente conjunto
\[ B=\{\beta a : a\in A\}, \quad C=\{\gamma+a: a\in A\}. \]Si \(A\) está acotado superiormente demuestra que \(B\) y \(C\) también están acotados superiormente y que
\[ \sup(B)=\beta \sup(A), \quad \sup(C)=\gamma+\sup(A) \]Notación: por simplicidad denotamos \[ \beta A := \{\beta a : a\in A\}, \quad \gamma+ A:=\{\gamma +a : a\in A\} \] Notar que esto es un abuso de notación, pues en \(\gamma +A\) por ejemplo, \(\gamma\) es un escalar pero \(A\) es un conjunto y el "resultado", \(\gamma+A\), es un conjunto.
Con ésta notación las fórmulas de éste ejercicio se pueden escribir \[ \sup(\beta A)= \beta\sup(A), \quad \sup(\gamma +A)=\gamma +\sup(A). \]
Hay fórmulas similares para el ínfimo: \[ \inf(\beta A)= \beta\inf(A), \quad \inf(\gamma +A)=\gamma +\inf(A). \]
Ejercicio
Sean \(A\) y \(B\) dos conjuntos no vacíos acotados superiormente. Define el conjunto: \[ A+B:=\{a+b| a\in A, b\in B\} \] Prueba que \(A+B\) está acotado superiormente y que \[ \sup(A+B)=\sup(A)+\sup(B) \]
Teorema
Cada número real no negativo tiene una única raíz cuadrada no negativa. Es decir, para todo \(a>0\) existe un único \(\alpha >0\) tal que \(\alpha^2=a\).
Existencia.
Fijamos \(a>0\) y definimos el conjunto \[ S=\{ x \geq 0: x^2 \leq a \}. \] Ya que \(0^2=0< a\), \(0\in S\) y por lo tanto \(S\ne \emptyset\). Además por el Ejercicio 3.4 \(S\) está acotado superiormente. Por lo tanto existe \(\alpha=\sup(S)\).
Afirmamos que \(\alpha >0\) y \(\alpha^2=a\).
Primero probamos \(\alpha >0\). Por el Ejercicio 3.11 existe \(n\in \mathbb{N}\) tal que \(\frac{1}{n}< a\) pero siempre si tiene que, para todo natural, \(\frac{1}{n^2} \leq \frac{1}{n}\) (pues \(\frac{1}{n}-\frac{1}{n^2}=\frac{(n+1)(n-1)}{n} \geq 0\)) por lo tanto \(\frac{1}{n^2} < a \), que se traduce en \(\frac{1}{n}\in S\) de lo que concluimos \(0< \frac{1}{n} \leq \sup(S)=\alpha \).
Resta probar \(\alpha^2 =a \). Primero suponemos que \(\alpha^2 < a\) y llegamos a una contradicción.
Vamos a encontrar un natural \(m\in \mathbb{N}\) tal que \((\alpha+\frac{1}{m})^2 < a\). Ya que estamos suponiendo que \(\alpha^2< a\), por el Ejercicio 3.11 existe \(m\in \mathbb{N}\) tal que \(\frac{1}{m}< \frac{a-\alpha^2}{2\alpha+1}\). Con esta \(m\) tenemos \begin{eqnarray*} \left(\alpha + \frac{1}{m} \right)^2 &=& \alpha^2+ \frac{2\alpha}{m} + \frac{1}{m^2} \\ &\leq & \alpha^2+ \frac{2\alpha}{m} + \frac{1}{m} \\ & < & \alpha^2+ \frac{2\alpha+1}{m} \\ &<& \alpha^2 +a -\alpha^2\\ &=& a \end{eqnarray*}
Por definición de \(S\), \(\alpha +\frac{1}{m} \in S\) de lo que se sigue \(\alpha+\frac{1}{m} \leq \sup(S)=\alpha\) lo que implica \(\frac{1}{m}\leq 0\), una contradicción. La contradicción vino de suponer \(\alpha^2 < a \) por lo tanto tenemos que \(a\leq \alpha^2\).
Finalmente probamos \(\alpha^2=a\). Por la propiedad fundamental del supremo, para toda \(\varepsilon \in (0,\alpha)\) existe \(x\in S\) tal \(\alpha-\varepsilon < x \leq \alpha\). Elevando al cuadrado llegamos a \((\alpha-\varepsilon)^2 < x^2 \leq \alpha^2\) pero también sabemos que \(a\leq \alpha^2\), asi que tenemos la cadena de desigualdades \[ (\alpha-\varepsilon)^2 < x^2 \leq a \leq \alpha^2 \] por lo que llegamos a \begin{eqnarray*} \alpha^2-a & \leq & \alpha^2-(\alpha -\varepsilon)^2\\ &=& \alpha^2-\alpha^2+2\alpha \varepsilon- \varepsilon^2 \\ & < & 2\alpha \varepsilon \end{eqnarray*} de lo cual obtenemos \[ 0\leq \frac{\alpha^2 -a}{2\alpha} < \varepsilon \] para todo \(\varepsilon\in (0, \alpha)\) lo cual implica que \(\frac{\alpha^2 -a}{2\alpha}=0\) y por lo tanto \(\alpha^2=a\).
Unicidad.
Supongasmos que existen \(\alpha>0 \) y \(\beta >0\) tal que \(\alpha^2=\beta^2=a\). Entonces por diferencia de cuadrados \[ \alpha^2-\beta^2=(\alpha-\beta)(\alpha+\beta) \] pero \(\alpha^2=\beta^2=a\) por lo que \(0=(\alpha-\beta)(\alpha+\beta)\) pero \(\alpha>0\) y \(\beta >0\) por lo que \(\alpha-\beta=0\), es decir \(\alpha=\beta\).
Ejercicio
Sean \(a>0,b>0\) con \(a< b\). Prueba que \(\sqrt{a}< \sqrt{b}\).
Sugerencia: \[ \sqrt{b}-\sqrt{a}=(\sqrt{b}-\sqrt{a})\left( \frac{\sqrt{b}+\sqrt{a}}{\sqrt{b}+\sqrt{a}}\right) \]
Definición
Dada \(a>0\) por \(\sqrt{a}\) denotamos al único número positivo cuyo cuadrado es \(a\). Por los dos ejercicios anteriores se asegura que, para toda \(a>0\), \(\sqrt{a}\) existe y es única.
Usando ideas similares a los dos ejercicios anteriores, se puede probar que para todo número \(a>0\) y todo natural \(n\geq 2\), existe un único real positivo, denotado \(\sqrt[n]{a}\), con la propiedad de que \((\sqrt[n]{a})^n=a\).
Una propiedad que es muy útil y que se probará más adelante es que si \(0< a < b\) entonces \(0< \sqrt[n]{a} < \sqrt[n]{b}\).
Ejercicio
Sea \(A\) un conjunto no vacío, acotado superiormente y contenido en \([0,\infty)\). Define el conjunto \[ A^2:=\{a^2: a\in A\}. \] Prueba que \(A^2\) está acotado superiormente y \[ \sup(A^2)=(\sup(A))^2. \]
Sugerencia: pudes usar que si \(0< a < b\) entonces \(0< a^2 < b^2\) y \(0 < \sqrt{a}< \sqrt{b}\).
Ejercicio
Fija \(a>0\). Si \(x\in \mathbb{R}\) satisface \(x^2=a\) demuestra que \(x=\sqrt{a}\) o que \(x=-\sqrt{a}\).
Ejercicio
Considera el rectangulo de base \(b\) y altura \(h\).
En el primer paso divide el rectangulo en 4 rectangulos iguales y denota por \(a_1\) al area del rectangulo inferior izquierdo.
En el segundo paso divide el rectangulo superior derecho en 4 partes iguales y denota por \(a_2\) al area del rectangulo inferior izquierdo.
Continua el proceso, como se ve en la figura.
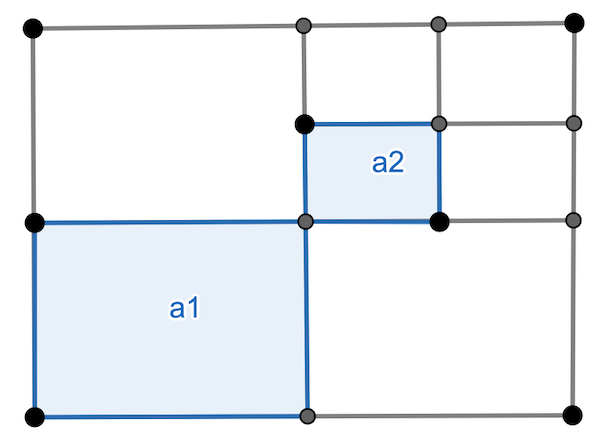
Construye el conjunto \[ A=\{ a_1, a_1+a_2, a_1+a_2+a_3, \dots \} \]
Encuentra el supremo de \(A\).
Sugerencia: Denota por \(a\) al area del rectángulo; usa un argumento geométrico para notar que
\begin{eqnarray*} 3a_1&=& a-\left(\frac{b}{2} \right) \left(\frac{h}{2}\right)\\ 3a_1+3a_2&=&a-\left(\frac{b}{2^2} \right) \left( \frac{h}{2^2} \right)\\ 3a_1+3a_2+3a_3&=&a-\left(\frac{b}{2^3}\right)\left(\frac{h}{2^3} \right) \end{eqnarray*}Ejercicio
Demuestra que \[ \sup \left\{ \sum_{k=1}^n \frac{1}{4^k}: n=1,2,\dots \right\}=\frac{1}{3} \] Sugerencia: usa un método similar al Ejercicio 3.23, usando un cuadrado de lado 1.Ejercicio
Considera un triángulo equilatero, de lado 1.
En el primer paso divide el triángulo en 4 triángulos equilateros congruentes y denota por \(a_1\) el area de dichos triángulo.
En el segundo paso divide uno de los triángulos del paso anterior en 4 triángulos congruentes y denota por \(a_2\) el area de dichos triángulos.
Continua el proceso y construye el conjunto \[ A=\{ a_1, a_1+a_2, a_1+a_2+a_3, \cdots \} \]
Demuestra \(\sup(A)=\frac{\sqrt{3}}{12}\).Sugerencia: usa un método parecido al Ejercicio 3.23.
Ejercicio
Prueba que \[ \sup\left( \left\{ 3-\frac{4}{n^2}+\frac{8}{n}: n=1,2,\dots \right\} \right)=7 \]
Proyecto
En este proyecto se prueba la existencia de raíces \(n\)-ésimas. En lo que sigue se fija \(n\geq 2\) un número natural y \(a >0\) un real positivo.
- Define \[ S=\{x \geq 0 : x^n \leq a \} \] Prueba que \(S\ne \emptyset\) y está acotado superiormente. Sugerencia: usa el Ejercicio 1.27 y el Ejercicio 1.28 también es útil.
- Define \(\alpha:= \sup(S)\) y prueba que \(\alpha > 0 \) y \(\alpha^n=a\).
- Para la unicidad supón que existe \(\beta >0\) tal que \(\beta^n=a\) y prueba que \(\alpha=\beta\). Sugerencia: Ejercicio 1.19