Continuidad
Introducción
Las funciones continuas son la estrellas en un primer curso de análisis matemático y uno de los objetivos principales del curso es tomar varias de las propiedades de las funciones continuas que se vieron en cálculo y extenderlas en el contexto de espacios métricos.
Hay dos puntos de vista importantes desde los cuales se pueden ver a las funciones continuas. Uno es desde el puntos de vista de sucesiones. Desde esta perspectiva las funciones continuas son las que mandan sucesiones convergentes en sucesiones convergentes. El otro punto de vista tiene que ver con las bolas abiertas y más en general con conjuntos abiertos. Vamos a presentar la definición de continuidad usando este último pero se verá más adelante que son equivalentes (Lema 9.4).
Definición
Sean \((X,d_X), (Y,d_Y)\) dos espacios métricos. Decimos que una función \(f;X\to Y\) es continua en un punto \(x_0\in X\) si:
para toda \(\varepsilon > 0\) existe \(\delta >0\), que depende de \(x_0\) y \(\varepsilon\), tal que si un punto \(x\in X\) está a distancia menor a \(\delta\) de \(x_0\), es decir \(d_X(x,x_0) <\delta\) entonces \(d_Y(f(x),f(x_0)) < \varepsilon\).
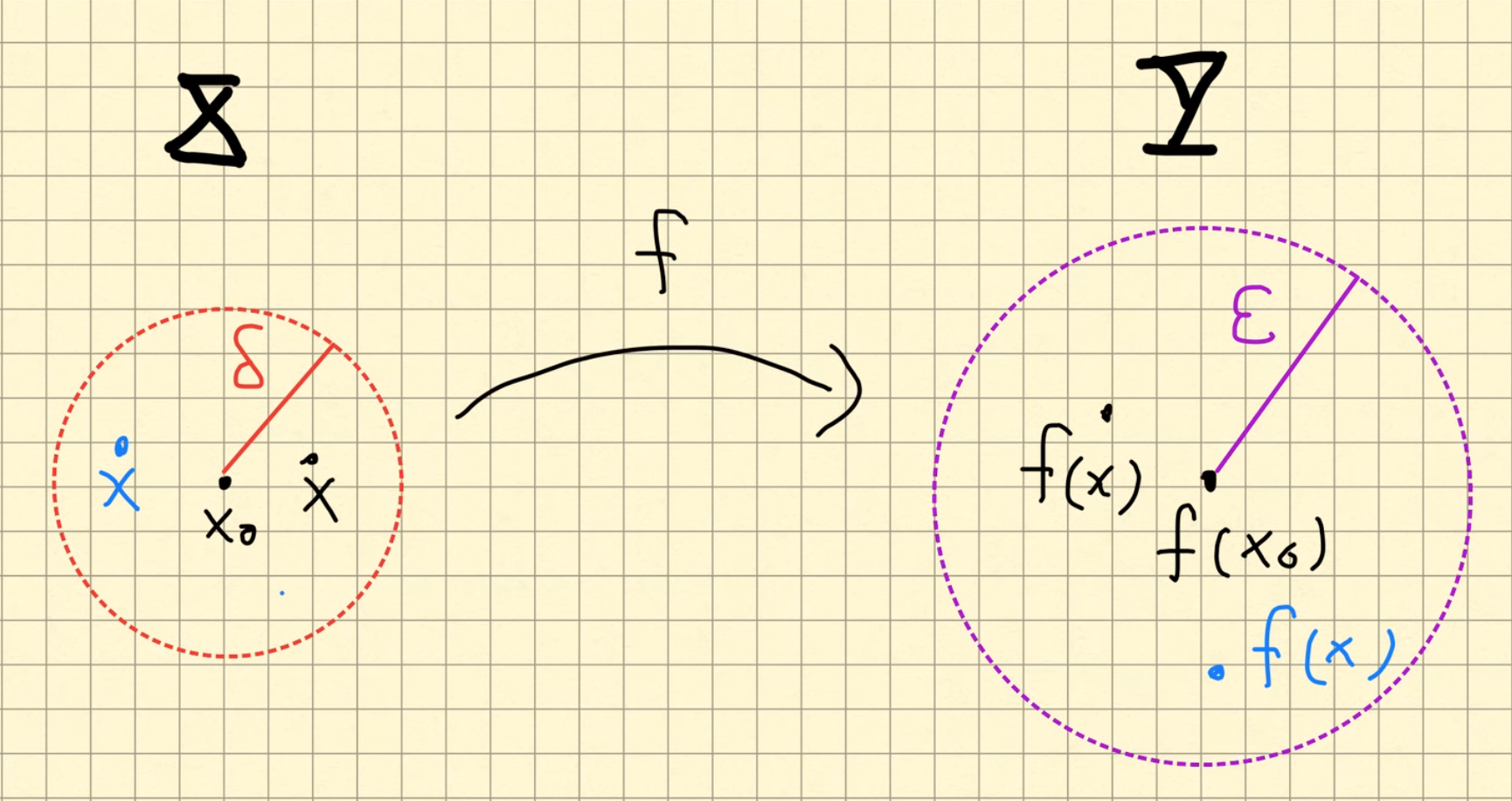
Nota que para probar que una función es continua en un punto, dada la \(\varepsilon\) todo el trabajo se enfoca en encontrar la \(\delta\) que satisfaga la condición dada arriba.
Usando la notación de bolas abiertas la definición se puede reescribir de la siguiente forma:
\(f\) es continua en \(x_0\) sii para toda \(\varepsilon >0 \) existe \(\delta >0\) que satisface \[ B^X_\delta(x_0) \subset f^{-1}(B^Y_\varepsilon(f(x_0))) \]
donde \(B^X_r(x_0)\) denota la bola abierta en el espacio \(X\).
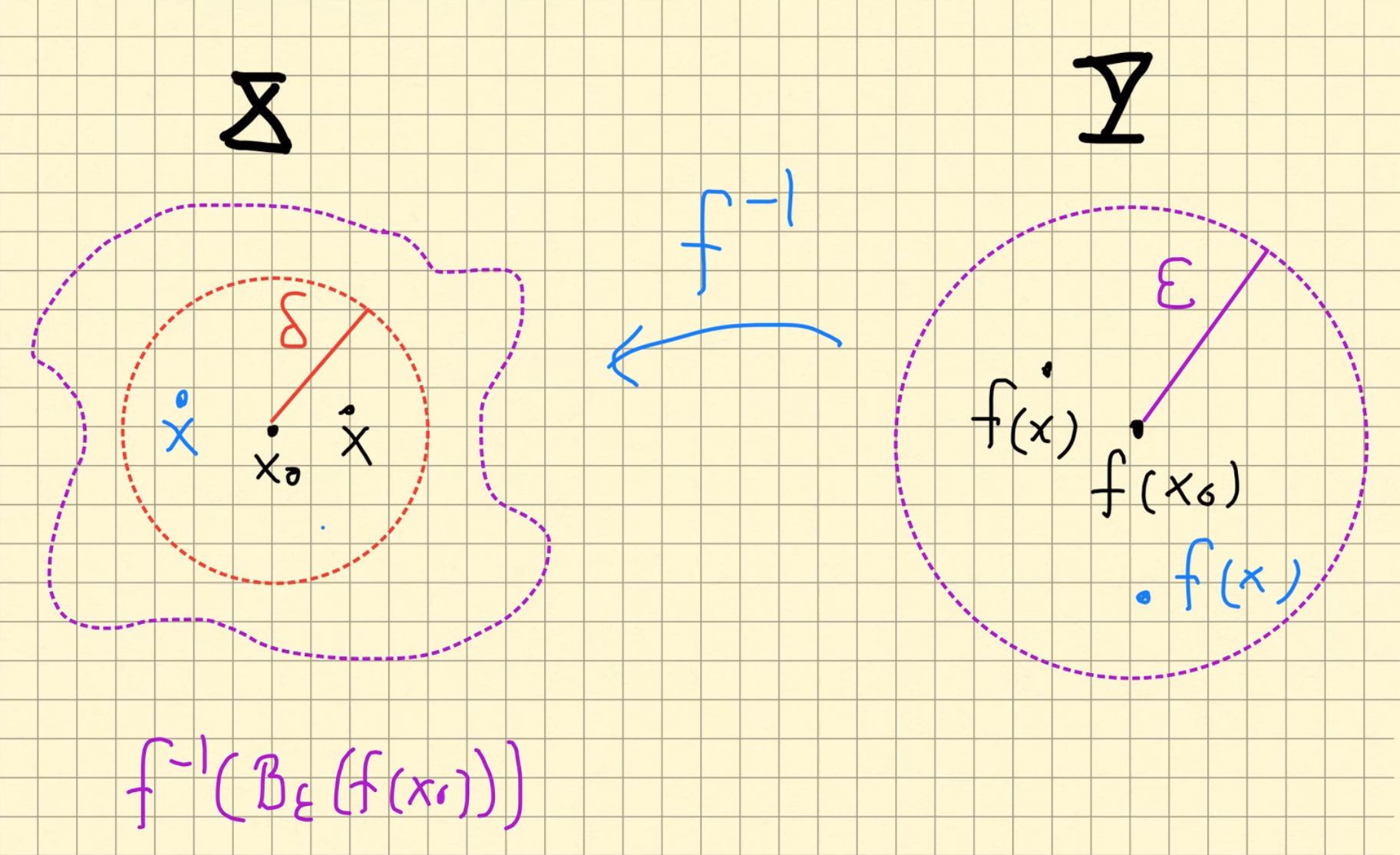
Nota: recuerda que en general, para una función \(f:X\to Y\), la imagen inversa de un subconjunto \(B\subseteq Y\), bajo \(f\) se define como: \(f^{-1}(B):=\{x\in X: f(x)\in B \}\).
Decimos que una función es continua en un subconjunto \(A \subseteq X\) si es continua en todo punto de \(A\).
Ejemplos
-
Toda función \(f:\mathbb{N}\to X\) es continua en todo punto de \(\mathbb{N}\),
considerando a éste útimo dotado con la métrica heredada de \(\mathbb{R}\)
y \(X\) cualquie espacio métrico.
Para ver lo anterior tomamos un punto cualquiera \(n_0\in \mathbb{N}\) y fijamos un número positivo \(\varepsilon\). En el caso muy particular de \(\mathbb{N}\) afirmamos que la \(\delta >0\) que nos sirve es \(\delta=1\). Razón: en la métrica de \(\mathbb{N}\) las bolas unitarias son muy simples \[ B_1(n_0)=\{n_0\} \] y por lo tanto para todo \(n \in B_1(n_0)\) (que sólo hay uno, \(n_0\)) se cumple \(d(f(n),f(n_0)) < \varepsilon\), pues \[ d(f(n),f(n_0))=d(f(n_0), f(n_0))=0. \] Nota: este ejemplo sigue siendo válido si intercambiamos \(\mathbb{N}\) por cualquier otro espacio métrico discreto.
-
Todas las isometrías son funciones continuas.
Recordamos que una isometría entre dos espacios métricos es una función que preserva las distancias, es decir una función \(f:(X,d_X) \to (Y,d_Y)\) que satisface \[ d_Y(f(x_1),f(x_2)) = d_X(x_1,x_2), \] para todos \(x_1,x_2\in X\).
Dado un punto cualquiera \(x_0\in X\) y un número positivo \(\varepsilon >0\) la \(\delta\) que sirve para la continuidad es \(\delta= \varepsilon\). En efecto, si \(d_X(x,x_0) < \delta \) entonces \[ d_Y(f(x),f(x_0))=d_X(x,x_0) < \delta = \varepsilon. \]
Ejercicio
Ya que la continuidad se puede escribir en términos de imágines inversas es útil tener varias propiedades sobre ésta.
Sean \(S,T\) dos conjuntos, \(f:S\to T\) una función y subconjuntos \(A,A' \subseteq S, B,B'\subseteq T\). Prueba las siguientes identidades de conjuntos
- \(A \subseteq f^{-1}(f(A))\) y la igualdad se da, para todo subconjunto \(A\) si y sólo si \(f\) es inyectiva.
- \(f(f^{-1}(B)) \subseteq B\) y la igualdad se da, para todo subconjunto \(B\) si y sólo si \(f\) es suprayectiva.
- \(f^{-1}(B\cap B')=f^{-1}(B)\cap f^{-1}(B')\).
- \(f^{-1}(B\cup B')=f^{-1}(B)\cup f^{-1}(B')\).
- \(f^{-1}(B\setminus B')=f^{-1}(B)\setminus f^{-1}(B')\).
- \(f(A\cup A')=f(A)\cup f(A')\).
- \(f(A\cap A') \subseteq f(A)\cap f(A')\). Además da un ejemplo dónde la contención sea propia.
- Si \(B'\subseteq B\) entonces \(f^{-1}(B')\subseteq f^{-1}(B)\).
Lema
Sean \((X,d_X), (Y,d_Y)\) dos espacios métricos y \(f:X \to Y\) una función.
Las siguientes condiciones son equivalentes.
- \(f\) es continua en \(x_0\).
- Para toda sucesión \((x_n)_{n=1}^\infty\) convergente a \(x_0\) se satisface que \((f(x_n))_{n=1}^\infty\) es convergente a \(f(x_0)\). Lo anterior se puede resumir como: \[ \lim_{n\to \infty} f(x_n)=f(\lim_{n\to \infty}x_n) \]
Es decir, se puede meter el límite para funciones continuar, siempre y cuando el límite exista.
\(\Rightarrow] \) Primero supongamos que \(f\) es continua en \(x_0\) y supongamos que tenemos una sucesión \((x_n)_{n=1}^\infty \subset X\) tal que \(\lim_{n\to \infty}x_n=x_0\).
Debemos probar que \(\lim_{n\to \infty }f(x_n)=f(x_0)\), es decir, dada una \(\varepsilon >0\) debemos asegurar la existencia de un natural \(N\in \mathbb{N}\) tal que, para toda \(n \geq N\): \begin{equation}\label{Eqn:auxLemaContinuidad} f(x_n)\in B_\varepsilon^Y(f(x_0)). \end{equation}
Usando que \(f\) es continua en \(x_0\), sabemos que existe una \(\delta >0 \) tal que \begin{equation}\label{Eqn:aux2LemaContinuidad} B_\delta^X(x_0) \subseteq f^{-1}(B_\varepsilon)(f(x_0)) \end{equation}
Pero, usando que \(\lim_{n\to \infty }x_n=x_0\) podemos asegurar que existe \(N\in \mathbb{N}\) tal que, para toda \(n\geq N\), \(x_n\in B_\delta^X(x_0)\). Si usamos \eqref{Eqn:aux2LemaContinuidad} obtenemos que \(f(x_n) \in B_\varepsilon(f(x_0))\), para toda \(n\geq N\), lo cual prueba \eqref{Eqn:auxLemaContinuidad}.
\(\Leftarrow]\) Vamos a proceder por contrapositiva. Supongamos que la función \(f\) no es continua en \(x_0\) y con esto vamos a probar que la condición 2 no es válida.
Si negamos la definición de continuidad de \(f\) en \(x_0\) llegamos a que existe un número positivo \(\varepsilon_0 >0 \), tal que, para toda \(\delta > 0\) no se cumple \[ B_{\delta}(x_0) \subseteq f^{-1}(B_{\varepsilon_0}(f(x_0))). \] Si la contención anterior no es válida eso quiere decir que existe un \(x \in B_{\delta}(x_0)\) (la \(x\) va a depender de \(\delta\)), tal que \(x\notin f^{-1}(B_{\varepsilon_0}(f(x_0)))\), es decir, la \(x\) satisface: \[ d_X(x,x_0)< \delta, \quad d_Y(f(x),f(x_0)) \geq \varepsilon_0. \]
Como lo anterior se vale para todo número \(\delta >0\), tomando \(\delta = \frac{1}{n}\), con \(n \in \mathbb{N}\), obtenemos una sucesión de puntos \((x_n)_{n=1}^\infty \subset X\), tal que \[ d_X(x_n,x_0) < \frac{1}{n}, \quad d_Y(f(x_n), f(x_0)) \geq \varepsilon_0 \] Pero lo anterior implica que \(\lim_{n\to \infty} x_n=x_0\) y \(\lim_{n\to \infty} f(x_n)\ne f(x_0)\), contradiciendo la condición 2 del lema.
Ejercicio
Sea \((X,d)\) un espacio métrico y \(f,g:X\to \mathbb{R}\) funciones continuas en \(x_0\in X\). Prueba que las siguientes funciones (dadas por operaciones algebráticas) son continuas en \(x_0\):
- combinaciones lineales \(\alpha f +g\), donde \(\alpha \in \mathbb{R}\),
- la función producto \(fg\),
- si \(g(x_0 )\ne 0\), la función cociente \(f/g\).
Sugerencia: usa el Lema 9.4
Nota: se puede generalizar este ejercicio cambiando \(\mathbb{R}\) por un espacio vectorial normado.
Lema
Sean \((X,d_X), (Y,d_Y)\) dos espacios métricos y \(f:X \to Y\) una función. Decimos que \(f\) es continua en \(X\) si \(f\) es continua en \(x_0\), para todo \(x_0\in X\).
Las siguientes condiciones son equivalentes.
- \(f\) es continua en todo \(X\).
- Imagen inversa de abiertos es abierta.
- Imagen inversa de cerrados es cerrada.
\(1 \Rightarrow 2 ]\) Supongamos que \(f\) es continua en todo \(M\) y sea \(V \subseteq Y\) un subconjunto abierto. Natamos que, al ser \(Y\) abierto, para todo \(y \in V \) existe \(r(y)\), un número positivo que depende de cada punto \(y\), tal que \(B_{r(y)}^Y(y)\subseteq V\). Por lo tanto se sigue que \[ V=\cup_{y\in V} B_{r(y)}^Y(y) \]
Usando las propiedades de la imagen inversa (Ejercicio 9.3) obtenemos \[ f^{-1}(V)=\cup_{y\in V} f^{-1}(B_{r(y)}^Y(y)) \] y ya que unión arbitraria de abiertos es abierta, para probar que \(f^{-1}(V)\) es abierta es suficiente probar que, para toda bola \(B_r^Y(y)\), su imagen inversa \(f^{-1}(B_r^Y(y))\) es abierta en \(X\).
Para probar que \(f^{-1}(B_r^Y(y))\) es abierto en \(X\) tomamos \(x\in f^{-1}(B_r(y))\) arbitrario y probamos que hay una bola centrada en \(x\) totalemente contenida en \(f^{-1}(B_r^Y(y))\). Antes de proceder notamos que \(f(x)\in B_r^Y(y)\) y ya que éste último es abierto existe \(s>0\) tal que \(B_s^Y(f(x)) \subseteq B_r^Y(y)\).
Ahora, ya que \(f\) es continua en todo \(X\), en particular \(f\) es continua en \(x\) por lo que existe una \(\delta >0\) para la cual se satisface \[ B_\delta^X(x) \subseteq f^{-1}(B_s(f(x))) \] Finalmente notamos que \[ B_s^Y(f(x))\subseteq B_r^Y(y) \Rightarrow f^{-1}(B_s^Y(f(x))) \subseteq f^{-1}(B_r^Y(y)) \] por lo tanto tenemos la cadena de contenciones \[ B_\delta^X(x) \subseteq f^{-1}(B_s^Y(f(x))) \subseteq f^{-1}(B_r^Y(y)) \] concluyendo que \(B_\delta^X(x)\) está totalmente contenida en \(f^{-1}(B_r^Y(y))\).
\( 2 \Rightarrow 3 ]\) Esta implicación es sencilla.
Supoongamos que \(F \subset Y\) es cerrado. Debemos probar que \(f^{-1}(F) \subseteq X\) es cerrado también o, equivalentemente, que \(X\setminus f^{-1}(F)\) es abierto en \(X\). Pero, por las propiedades de la imagen inversa (Ejercicio 9.3): \[ X\setminus f^{-1}(F) = f^{-1}(Y \setminus F). \] Ahora, \(Y\setminus F\) es abierto en \(Y\), por lo tanto la condición 2 implica que \(f^{-1}(Y\setminus F)\) es abierto en \(X\).
\(3 \Rightarrow 1 ]\) Sea \(x_0 \in X\) fijo y arbitrario. Dedemos de probar que \(f\) es continua en \(x_0\) y para esto usaremos el Lema 9.4.
Sea \((x_n)_{n=1}^\infty \subset X\) una sucesión tal que \(\lim_{n\to \infty} x_n=x_0\). Debemos de probar que \(\lim_{n\to \infty} f(x_n)=f(x_0)\), pero, para llegar a una contradicción supongamos que no es así.
Usando el Ejercicio 5.18 sabemos \(\lim_{n\to \infty}f(x_n)\ne f(x_0)\) implica la existencia de un número positivo \(\varepsilon_0 >0\) y una subsucesión \((x_{n_k})_{k=1}^\infty\) tal que \[ d(f(x_0), f(x_{n_k})) \geq \varepsilon_0 \] para toda \(k\). Reescribiendo lo anterior en términos de imagen inversa de la bola abierta tenemos que \[ x_{n_k} \in f^{-1}(Y\setminus B_{\varepsilon_0}(f(x_0))) \] para toda \(k\).
Por otro lado, sabemos que \(Y\setminus B_{\varepsilon_0}(f(x_0)) \) es cerrado, por lo tanto la condición 3 implica que \(f^{-1}(Y\setminus B_{\varepsilon_0}(f(x_0))\) también es cerrado. Por lo tanto la subsucesión \((x_{n_k})_{k=1}^\infty\) está contenida en el cerrado \(f^{-1}(Y\setminus B_{\varepsilon_0}(f(x_0))\) y en consecuencias, su límite también (por Teorema 6.14). Es decir \[ x_0=\lim_{k\to \infty}x_{n_k} \in f^{-1}(Y\setminus B_{\varepsilon_0}(f(x_0)) \] por lo que \(f(x_0)\in Y\setminus B_{\varepsilon_0}(f(x_0)) \), lo cual es una contradicción.
Lema
Sea \(f:(X,d_X)\to (Y,d_Y)\) una función continua y \(K \subseteq X\) un subconjunto compacto. Prueba que \(f(K)\subseteq Y \) es compacto.
Sea \(\{U_\alpha\}_{\alpha \in \Lambda }\) una cubierta abierta de \(f(K)\).
Afirmamos que \(\{f^{-1}(U_\alpha)\}_{\alpha \in \Lambda}\) es una cubierta abierta de \(K\). Razón: ya que \(f\) es continua y \(U_\alpha \subseteq Y\) es abierto se sigue que \(f^{-1}(U_\alpha)\subseteq X\) es abierto. Ahora probamos la contención \(K\subseteq \cup_{\alpha \in \Lambda} f^{-1}(U_\alpha)\): dado \(x\in K\) se sigue \[ f(x)\in f(K) \subseteq \cup_{\alpha \in \Lambda} U_\alpha \] por lo que existe un índice \(\alpha_0\) para el cual \(f(x)\in U_{\alpha_0}\) lo cual implica \(x\in f^{-1}(U_{\alpha_0})\).
Como \(K\) es compacto y \(\{f^{-1}(U_\alpha)\}_{\alpha \in \Lambda}\) es una cubierta abierta, existen índices \(\alpha_1,\dots, \alpha_n\) para los cuales \begin{equation}\label{Eqn:AuxImagenDeCompactoEsCompacto} K\subseteq \cup_{i=1}^n f^{-1}(U_{\alpha_i}) \end{equation}
Resta probar que \(f(K)\subseteq \cup_{i=1}^n U_{\alpha_i}\). Dado \(y\in f(K)\), existe \(x\in K\) tal que \(y=f(x)\). Por la contención \eqref{Eqn:AuxImagenDeCompactoEsCompacto} existe \(\alpha_{i_0}\) tal que \(x\in f^{-1}(U_{\alpha_{i_0}})\) lo cual implica \(y=f(x)\in U_{\alpha_{i_0}}\).
Teorema
Sea \((X,d)\) un espacio métrico, \(K\subseteq X\) compacto y \(f:K \to \mathbb{R}\) una función continua en \(K\). Entonces \(f\) alcanza su máximo y su mínimo en \(K\), es decir, existen puntos \(x_*,x^*\in K\) tales que, para todo \(x\in K\) \[ f(x_*) \leq f(x) \leq f(x^*). \] En notación: \(\min_{x\in X}\{f(x)\}=f(x_*), \max_{x\in X}\{f(x)\}=f(x^*)\)
Por el Lema 9.7, \(f(K)\) es un subconjunto compacto de \(\mathbb{R}\), por lo tanto \(f(K)\) es cerrado y acotado. Por lo tanto existen \[ \alpha = \sup(f(K)), \beta= \inf(f(K)) \] Por las propiedades fundamentales del ínfirmo y supremo existen sucesiones \((y_n)_{n=1}^\infty, (z_m)_{m=1}^\infty \subset K\) tales que \begin{equation}\label{Eqn:Aux1MaxMinFunContinuasCompactos} \lim_{n\to \infty} f(y_n)=\alpha, \lim_{m\to \infty} f(z_m)=\beta. \end{equation}
Por el Teroema 7.12, existen subcuseciones \((y_{n_k})_{k=1}^\infty \), \((z_{m_j})_{j=1}^\infty\) y puntos \(x_*, x^*\in K\) tales que \[ \lim_{k\to \infty} y_{n_k}=x_*, \quad \lim_{j\to \infty} z_{n_j}=x^* \] y por la continuidad de \(f\) en \(K\) concluimos \begin{equation}\label{Eqn:Aux2MaxMinFunContinuasCompactos} \lim_{k\to \infty} f(y_{n_k})=f(x_*), \lim_{j \to \infty} f(z_{m_j})= f(x^*). \end{equation}
Comparando \eqref{Eqn:Aux1MaxMinFunContinuasCompactos}, \eqref{Eqn:Aux2MaxMinFunContinuasCompactos} concluimos \[ f(x_*)=\alpha = \inf(f(K)), f(x^*)=\beta =\sup(f(K)) \] por lo que \[ f(x_*)\leq f(x) \leq f(x^*) \] para todo \(x\in K\).
Ejercicio
Sea \(f:[a,b]\to \mathbb{R}\) función continua. Entonces la imagen de \(f\) es un intervalo de la forma \([c,d]\), para algunos \(c,d\in \mathbb{R}\).
Ejercicio
Sea \((X,d)\) un espacio métrico y fija un punto \(y\in X\). Define \(f:X\to \mathbb{R}\) por \(f(x)=d(x,y)\). Prueba que \(f\) es continua en todo \(X\).
Sugerencia: Ejercicio 4.17
Ejercicio
Sea \((X,d)\) un espacio métrico y \(K \subset X\) un subconjunto compacto. Prueba que \(\operatorname{diam}(K)\) es finito. Es más, si \(K\ne \emptyset\), prueba que existen \(x,y\in K\) tal que \(\operatorname{diam}(K)=d(x,y)\).
Ejercicio
Cualesquiera dos normas en \(\mathbb{R}^n\) son equivalentes.
Empecemos por notar que la relación de 'ser norma equivalente' es una relación de equivalencia. Si \(\| \|\) es una norma, claramente \(\|x\| \leq 1 \cdot \|x\|\) para todo \(x \in X\), por lo que la relación es reflexiva. De la definición de norma equivalente también tenemos de forma inmediata que la relación es simétrica. Si \(\|\|_1, \|\|_2, \|\|_3\) son normas equivalentes entonces existen \(c_1,d_1,c_2,d_2 >0\) tales que para todo \(x \in X\) \[\|x\|_1 \leq c_1\|x\|_2, \quad \|x\|_2 \leq d_1 \|x\|_1\] y \[\|x\|_2 \leq c_2\|x\|_3, \quad \|x\|_3 \leq d_2 \|x\|_2,\] de donde \[\|x\|_1 \leq (c_1c_2)\|x\|_3, \quad \|x\|_3 \leq (d_1d_2) \|x\|_1,\] y tenemos que la relación es transitiva.
Una vez que lo anterior ha sido establecido será suficiente demostrar que toda norma en \(\mathbb{R}^n\) es equivalente a la norma \(\|\|_\infty\) en \(\mathbb{R}^n\).
Consideremos la base canónica en \(\mathbb{R}^n\), \(\{e_1,...,e_n\}\), y sea \(x \in \mathbb{R}^n\). Entonces \(x = (x_1,...,x_n) = x_1 e_1 + ... + x_n e_n\). Definimos \(0 < C = \max \{||e_i||:1 \leq i \leq n\}\) y tenemos lo siguiente: \[ ||x|| = ||x_1 e_1 + ... + x_n e_n|| \leq \sum_{i=1}^n |x_i| ||e_i|| \leq C \sum_{i=1}^n |x_i| \leq C ||x||_\infty \]
Para mostrar la segunda desigualdad tendremos que observar varias cosas:
- El conjunto \(S = \{x : ||x||_\infty = 1\}\) es compacto en \((\mathbb{R}^n,||||_\infty)\). Como \(||x||_\infty \leq ||x||_2 \leq \sqrt{n}||x||_2\) entonces \(||x||_2 \leq \sqrt{n}\) para todo \(x \in S\) y \(S\) es acotado. \(S\) es cerrado bajo la norma \(||||_\infty\), y como \(||||_2\) y \(||||_\infty\) son equivalentes, también es cerrado bajo \(||||_2\). Por el Teorema de Heine-Borel tenemos que es compacto en la topología inducida por la norma \(||||_2\), pero al ser equivalente a la norma \(||||_\infty\) también es compacto respecto a \(||||_\infty\).
- La norma \(||||\) es una función continua \(||||:\mathbb{R}^n \to \mathbb{R}\) respecto a la norma \(||||_\infty\). Como \(||||\) es norma entonces satifsface la desigualdad del triángulo inversa. Si además utilizamos la desigualdad mostrada en la primera parte de la prueba tenemos lo siguiente: \[ |||x||-||y||| \leq ||x-y|| \leq C ||x-y||_\infty. \] Si \(\epsilon >0\) entonces podemos tomar \(\delta = \epsilon / C\) como testigo de la continuidad de \(||||\).
- Como \(S\) es compacto y \(||||\) es continua, entonces \(||||\) alcanza un mínimo en \(S\), llamemos \(x_0\) a un punto donde se alcanza dicho mínimo. Sea \(x \in \mathbb{R}^n\). Si \(x=0\) entonces \(0=||x||_\infty \leq D ||x|| = 0\) para toda \(D\in \mathbb{R}\). Supongamos ahora que \(x \neq 0\), entonces \(||x||_\infty > 0\) y \(x/{||x||_\infty} \in S\). Por definición de \(x_0\) se tiene que \(||x_0|| \leq ||x/||x||_\infty|| = \frac{||x||}{||x||_\infty}\) y en consecuencia \(||x||_\infty \leq \frac{1}{||x_0||}||x||\), por lo que si \(D=1/||x_0||\) entonces \(||x||_\infty \leq D ||x||\) y hemos probado lo que las normas son equivalentes.
Ejercicio
Sea \(A \subset \mathbb{R}^n\) un cerrado y \(x\notin A\). Prueba que existe un \(a_*\in A\) tal que \[ d(x,A)=d(x,a_*) \]
Ejercicio
- Prueba que una función continua \(f:\mathbb{R}\to \mathbb{R}\) está completamente determinada por sus valores en \(\mathbb{Q}\). Es decir, si \(g:\mathbb{R}\to \mathbb{R}\) es una función continua que satisface \(f(r)=g(r)\) para toda \(r\in \mathbb{Q}\) entonces \(f(x)=g(x)\) para toda \(x\in \mathbb{R}\).
-
Generaliza el ejercicio anterior. Sean \((X,d_X), (Y,d_Y)\) dos espacios métricos y sea \(D\subset X\) un subconjunto denso. Prueba que una función continua \(f:X \to Y\) está completamente determinada por sus valores en \(D\).
Sugerencia: usa el Ejercicio 6.34 inciso 2.
- Como \(f,g\) coinciden en \(\mathbb{Q}\) bastará probar que también coinciden en los irracionales \(\mathbb{I}\). Recordemos que todo número irracional es el límite de una sucesión de números racionales. Con esto establecido usaremos el Lema anterior. Sea \(x\) un número irracional y \((x_n)_n\) una sucesión de racionales tal que \(\lim x_n= x\). Por hipótesis \(f(x_n) = g(x_n)\) para cada \(n \in \mathbb{N}\) y por continuidad de las funciones \(f,g\) en el punto \(x\) tenemos que \(f(x) = \lim f(x_n) = \lim g(x_n) = g(x)\). En consecuencia \(f(x) = g(x)\) para todo \(x \in \mathbb{R}\).
Ejercicio
Sea \(f:\mathbb{R}\to \mathbb{R}\) que satisface: \(f(x+y)=f(x)+f(y)\), para todos \(x,y\in \mathbb{R}\).
Prueba que si \(f\) es continua en un punto entonces existe una constante \(a\in \mathbb{R}\) tal que \(f(x)=ax\) para todo \(x\in \mathbb{R}\).
Es decir, toda función aditiva y continua en almenos un punto es lineal.
Sugerencia: empieza probando que si \(f\) es aditiva y continua en un punto entonces es continua en cero y después prueba que es continua en todo punto.
Ejercicio
Sea \((X,d)\) un espacio métrico y \(f:X\to \mathbb{R}\) una función.
- Si \(f\) es continua en \(X\) entonces, para todo \(a\in \mathbb{R}\) entonces \(\{x: f(x)>a\}\) y \(\{x: f(x)< a \}\) son abiertos.
- Inversamente, si para toda \(a\in \mathbb{R}\) se satisface que \(\{x: f(x)>a\}\) y \(\{x: f(x)< a \}\) son conjuntos abiertos prueba que \(f\) es continua en \(\mathbb{R}\).
- Mejora el inciso anterior. Prueba que si para toda \(a\in \mathbb{Q}\) se satisface que \(\{x: f(x)>a\}\) y \(\{x: f(x)< a \}\) son conjuntos abiertos prueba que \(f\) es continua en \(\mathbb{R}\).
Sugerencia: usa el Lema 9.6.
Ejercicio
Sean \((X,d_X), (Y,d_Y)\) dos espacios métricos y \(f:X\to Y\) una función. La gráfica de \(f\) se define como el subconjunto de \(X\times Y\) dado por \[ G(f):=\{(x,f(x)): x\in X\} \]
- Prueba que \(f\) es continua en \(X\) entonces \(G(f)\) es un subconjunto cerrado de \(X\times Y\).
- Da un ejemplo donde \(G(f)\) sea cerrado pero \(f\) no es continua.
Nota: considera el espacio \(X\times Y\) dotado con la métrica \(d((x_1,y_1),(x_2,y_2))=d_X(x_1,x_2)+d_Y(y_1,y_2)\).
Ejercicio
Sea \(f:\mathbb{R}\to \mathbb{R}\) una función y define \(F:\mathbb{R}\to \mathbb{R}^2\) por \(F(x)=(x,f(x))\). Prueba que las siguientes condiciones son equivalentes.
- \(f\) es continua en \(\mathbb{R}\).
- \(F\) es continua en \(\mathbb{R}\).
- Los subconjuntos \[ \{(x,y)\in \mathbb{R}^2: y \leq f(x) \}, \quad \{(x,y)\in \mathbb{R}^2: f(x)\leq y\} \] son cerrados en \(\mathbb{R}^2\).
Ejercicio
Una función entre dos espacio métricos \(f: X \to Y\) se dice que satisface la condición de Lipschitz si existe un constante \(K>0\) para la cual: \[ d_Y(f(a),f(b)) \leq K d_X(a,b), \quad \textrm{para todos \(a,b\in X\)}. \] Por sencillez también se dice que \(f\) es Lipschitz con constante \(K\).
- Prueba que toda función Lipschitz es continua en todo punto.
- Mejora el inciso anterior. Prueba que toda función Lipschitz es uniformemente continua en su dominio.
Nota: una función \(g:X\to Y\) se llama uniformemente continua en \(X\) si para toda \(\varepsilon >0\) existe una \(\delta>0\), que sólo depende de \(\varepsilon\), tal que \[ d_X(a,b) < \delta \Rightarrow d_Y(g(a),g(b))<\varepsilon \]
Ejercicio
- Prueba que las funciones \(\sen, \cos:\mathbb{R}\to \mathbb{R}\) son Lipschitz con constante \(K=1\).
- Generaliza el inciso anterior. Si \(f:[a,b]\to \mathbb{R}\) es continua en \([a,b]\), diferenciable en \((a,b)\) y con derivada acotada en \((a,b)\) entonces \(f\) es Lipschitz.
-
Comencemos por recordar el Teorema del Valor Medio. Si \(f:[a,b] \to \mathbb{R}\) es continua en \([a,b]\) y diferenciable en \((a,b)\) entonces existe un punto \(c \in (a,b)\) tal que \(f'(c) = \frac{f(b)-f(a)}{b-a}\).
Dado que \(\sen\) y \(\cos\) son continuas y diferenciables en todo \(\mathbb{R}\). Trabajaremos con \(\sen\) y el caso para \(\cos\) será análogo. Recordemos que ambas funciones toman valores en el intervalo \([0,1]\) y \(\sen '(x) = \cos(x)\), de esta forma si \(a,b \in \mathbb{R}\) entonces existe \(c \in (a,b)\) tal que \(\cos(c) = \frac{\sen(b)-\sen(a)}{b-a}\). Basta tomar valor absoluto en ambos lados de la ecuación y despejar el término \(|b-a|\) para obtener \(|\sen(b) - \sen(a)| = |\cos(c)||b-a|\). Como \(|\cos(c)| \leq 1\) concluimos que \(|\sen(b) - sen(a)| \leq 1 \cdot |b-a|\) y la función en cuestión es Lipschitz con constante \(K=1\). El caso de \(\cos\) es análogo. Dados \(a,b \in \mathbb{R}\) existe \(c \in (a,b)\) tal que \(|\cos(b) - \cos(a)| = |-\sen(c)||b-a| \leq 1 \cdot |b-a|\).
- Notemos que la generalización la obtenemos de manera natural de la demostración anterior. Supongamos que \(|f'(z)| \leq K \). Sean \(x,y \in [a,b]\) y supongamos SPG que \(x < y\). Por el Teo. del Valor Medio sabemos que existe \(z \in (x,y) \subseteq (a,b)\) tal que \(f'(z) = \frac{f(y) - f(x)}{y - x}\). Tomando valor absoluto de ambos lados de la ecuación y despejando el término \(|y-x|\) tenemos \(|f(y) - f(x)| = |f'(z)||y - x| \leq K |y-x|\), por lo que la función es Lipschitz.
Ejercicio
Considera la función \(L: \ell_\infty \to \mathbb{R}\) dada por \[ L(x)=\sum_{n=1}^\infty \frac{1}{2^n} x_n \] donde consideramos \(\ell_\infty\) dotado con la norma \(\|\cdot\|_\infty\).
Prueba que \(L\) es Lipschitz.
Ejercicio
-
Fija \(y=(y_n)_{n=1}^\infty \in \ell_2\) y define \(g:\ell_2 \to \mathbb{R}\) por \[ g(x)=\sum_{n=1}^\infty x_ny_n \] Por la desigualdad de Cauchy-Schwartz \(g\) está bien definida, es decir, la serie \(\sum_{n=1}^\infty x_ny_n\) es convergente.
Prueba que \(g\) es Lipschitz.
- Generaliza el inciso anterior. Sean \(p,q\in (1,\infty)\) exponentes conjugados y fija \(y\in \ell_q \). Define \(g:\ell_p \to \mathbb{R} \) por \[ g(x)=\sum_{n=1}^\infty x_ny_n \] Prueba que \(g\) es Lipschitz. Sugerencia: usa la desigualdad de Hølder.
Ejercicio
Sean \((X,d_X), (Y,d_Y)\) dos espacios métricos. Una función \(f:X \to Y\) se llama isometría si para todos \(a,b\in X\) \[ d_X(a,b)=d_Y(f(a),f(b)). \]
- Prueba que la función \(F: \mathbb{N} \to \ell_1\) dada por \[ F(n)=(\underbrace{1,\dots,1}_{n \quad \textrm{lugares}}, 0, 0, \dots) \] es una isometría. Nota: \(\mathbb{N}\) está dotado con la métrica usual heredada de \(\mathbb{R}\).
- Sea \(p\in [1,\infty) \). Define \(G: \ell_p \to \ell_p\) dada por \[ G((x_1,x_2,\dots, ))=(0,x_1,x_2,\dots) \] Prueba que \(G\) es una isometría.
Ejercicio
Sea \((X,d)\) un espacio métrico y \(A\subseteq X\). La distancia de un punto \(x\in X\) al conjunto \(A\) se define como \[ d(x,A):=\inf_{a\in A}\{ d(x,a) \} \] Prueba que \(|d(x,A)-d(y,A)|\leq d(x,y)\), para todos \(x,y\in X\).
Por lo tanto la función distancia a un conjunto es Lipschitz continua con \(K=1\).
Ejercicio
Sea \((X,d)\) un espacio métrico y \(E,F \subseteq X\) dos conjuntos cerrados, no vacíos y ajenos. Define \(f:X\to \mathbb{R}\) por \[ f(x)=\frac{d(x,E)}{d(x,E)+d(x,F)} \]
- Prueba que \(f\) es continua.
- Para toda \(x\in X\), \(0\leq f(x)\leq 1\).
- \(f^{-1}(0)=E\), \(f^{-1}(1)=F\).
Sugerencia: usa Ejercicio 9.24 y Ejercicio 6.33
Usa lo anterior prueba que existen dos conjuntos abiertos, \(U,V\), ajenos con \(E\subset U\), \(F \subset V\). Se dice que los conjuntos \(U\) y \(V\) separan a \(E\) y \(F\).
Ejercicio
Una función definida sobre un espacio métrico, con valores en \(\mathbb{R}\), \(f:X\to \mathbb{R}\) se llama semi-continua inferiormente si para toda \(a\in \mathbb{R}\) el conjunto \[ \{x\in X: f(x)\leq a \} \] es cerrado.
Prueba que \(f\) es semi-continua inferiormente si y sólo si \[ f(x)\leq \liminf_{n\to \infty} f(x_n) \] siempre que \(\lim_{n\to \infty} x_n=x\).
Nota: para una sucesión de números reales \((r_n)_{n=1}^\infty\) se define \[ \liminf_{n\to \infty} r_n = \sup_{n\geq 1} \left\{ \inf_{k\geq n} \{r_k\} \right\} \]
Definicion
Un homeomorfismo entre dos espacios métricos, \((X,d_X), (Y,d_Y)\), es una función \(f: X\to Y\) que satisface:
- \(f\) es inyectiva.
- \(f\) es suprayectiva.
- Tanto \(f\) como su inversa, \(f^{-1}\), son funciones continuas.
Si existe un homeomorfismo entre los espacios \(X\) y \(Y\) se dicen que son homeomorfos.
Ejemplo
- Cualquier función \(f:(-1,1)\to \mathbb{R}\) de la forma \(f(x)=\frac{x}{1-x^2}\), es un homeomorfismo entre \((-1,1)\) y \(\mathbb{R}\).
- Toda isometría \(f:(X,d_X)\to (Y,d_Y)\) suprayectiva es un homemomorfismo.
Ejercicio
Sea \((X,d_X)\) un espacio métrico compacto.
Supón que \(f: (X,d_X) \to (Y,d_Y)\) es una función continua, inyectiva y suprayectiva. Prueba que \(f\) es un homeomorfismo.
Nuestras hipótesis incluyen continuidad y biyectividad de la función \(f\), únicamente es necesario demostrar que \(f^{-1}\) también es continua. Por el Lema bastará demostrar que si \(C\subseteq X\) es cerrado, entonces \(((f^{-1})^{-1}(C))=f(C)\) es cerrado. Sea \(C \subseteq X\) un conjunto cerrado, como \(X\) es compacto entonces \(C\) también es compacto. Dado que \(f\) es continua y \(C\) es compacto \(f(C)\subseteq Y\) también es compacto. Para concluir demostraremos que en un espacio métrico los subconjuntos compactos son cerrados.
Sea \(K \subseteq X\) compacto y \((x_n)_{n=1}^\infty\) una sucesión en \(K\) que converja a un punto \(x \in X\). Por Lema \((x_n)_{n=1}^\infty\) admite una subsucesión \((x_{n_k})_{k=1}^\infty\) que converge a un punto \(y \in K\). Recordemos que si una sucesión es convergente entonces toda subsucesión converge al mismo punto, por lo que \(x=y\in K\) y \(K\) es cerrado.
Ejercicio
Sean \((X,d_X), (Y,d_Y)\) espacios métricos y \(f:X\to Y\) una biyección. Las siguientes condiciones son equivalentes.
- \(f\) es un homemorfismo.
- \(U\) abierto en \(X\) si y sólo si \(f(U)\) abierto en \(Y\).
- \(F\) cerrado en \(X\) si y sólo si \(f(U)\) cerrado en \(Y\).
- una sucesión \((x_n)_{n=1}^\infty \subseteq X\) satisface \(\lim_{n\to \infty}x_n=x\) en \(X\) si y sólo si la sucesión \((f(x_n))_{n=1}^\infty\subseteq Y\) satisface \(\lim_{n\to \infty} f(x_n)=f(x)\) en \(Y\).
Ejercicio
Sea \(X \ne \emptyset\) un conjunto y \(d,\rho\) dos métricas sobre \(X\).
Prueba que las métricas \(d\) y \(\rho\) son equivalentes si y sólo si la función identidad \(\operatorname{id}: (X,d) \to (X,\rho)\) es un homemorfismo.
Ejercicio
Por \((X,d)\) denotamos al espacio métrico \(X=\{0\} \cup \{\frac{1}{n}: n=1,2,\dots \}\) donde \(d \) es la métrica usual, heredada de \(\mathbb{R}\).
En \(X\) define una nueva métrica dada por \[ \rho(x,y)=\left\{ \begin{array}{cc} \left| \frac{1}{n}-\frac{1}{m} \right| & \textrm{si \(x=1/n, y=1/m\) con \(n,m\geq 2\)}\\ \frac{1}{n} & \textrm{si \(y=1\), \(x=1/n\) con \(n\geq 2\)} \\ 1-\frac{1}{n} & \text{si \(y=0\), \(x=1/n\) con \(n\geq 2\))} \\ 1 & \textrm{si \(y=0\), \(x=1\)} \end{array} \right. \]
Prueba que \((X,d)\) y \((X,\rho)\) son homemomorfos y que la función identidad \(\operatorname{id}:X \to X\) no es continua.
Ejercicio
Sea \((V,\|\cdot\|)\) un espaio vectorial normado. Prueba que \(V\) y \(B_1(0)\) son homeomorfos.
Hint: considera la función \(f: V\to B_1(0)\) dada por \(f(x)=\frac{1}{1+\|x\|}x\).
Ejercicio
Sea \(f:\mathbb{R}\to \mathbb{R}\) una función continua.
Fija \(a\in \mathbb{R}\). Prueba que el conjunto \(\{t\in \mathbb{R}: f(t)>a\}\) es abierto y que \(\{ t\in \mathbb{R}: f(t)=a\}\) es cerrado.
Como \(f(t) > a\) entonces podemos tomar \(\epsilon = \frac{1}{2}|f(t)-a|\). Por continuidad de \(f\) existe \(\delta > 0\) tal que si \(|t-s| < \delta\) entonces \(|f(t)-f(s)| < \epsilon\). Ésto último se puede reescribir como, si \(s \in B_{\delta}(t)\), entonces \(|f(t)-f(s)|< \epsilon\). En particular, por definición de \(\epsilon\) se tiene que \(f(s) > a\) y que \(B_{\delta}(t) \subseteq \{t \in \mathbb{R}: f(t) > a\}\).
Como consecuencia de lo anterior tenemos que \(\{t \in \mathbb{R}: f(t) \leq a\}\) es un conjunto cerrado. Se puede demostrar que \(\{t \in \mathbb{R}: f(t)< a\}\) también es un conjunto abierto (una opción es definir \(g(t) = -f(t)\) y aplicar el resultado), por lo que \({t \in \mathbb{R}: f(t) \geq a}\) también es cerrado y como \[ \{t \in \mathbb{R} : f(t) = a\} = \{t \in \mathbb{R}: f(t) \geq a\} \cap \{t \in \mathbb{R} : f(t) \leq a\} \] concluimos que el conjunto es cerrado.
Quiz
-
(3 pts) Considera el espacio \((\ell_2,\|\cdot\|_2)\). Prueba que el conjunto \[ A=\{x\in \ell_2: \sum_{n=1}^{\infty} \frac{x(n)}{n} >0\} \] es abierto.
-
(2 pts) Considera el espacio \((C([a,b]), \|\cdot\|_1)\) (ver quiz de la sección 3). Fija una función \(h_0\in C([a,b])\). Define la función \(L:C([a,b])\to \mathbb{R}\) por \[ L(f)=\int_a^b f(t)h_0(t)dt. \] Prueba que \(L\) es Lipschitz continua.
Quiz
-
(3 pts) Sean \((X,d_X)\), \((Y,d_Y)\) espacios métricos con \(X\) compacto y sea \(f:X\to Y\) una función continua. Prueba que \(f\) es cerrada.
Nota: una función se llama cerrada si manda cerrados en cerrados. Es decir, si \(F \subseteq X\) es cerrado entonces \(f(F)\subseteq Y\) es cerrado.
Quiz
- Prueba o da un contraejemplo: si \((X,d_X), (Y,d_Y)\) son espacios métricos y \(A\subseteq X\) es totalmente acotado y \(f:X\to Y\) es continua entonces \(f(A)\) es totalmente acotado.
- Prueba o da un contraejemplo: si \((X,d_X), (Y,d_Y)\) son espacios métricos con \(X\) completo y \(f:X\to Y\) es una función continua entonces \(f(X)\) es completo.